Question

Find the domain of the function f which is defined as $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$?
(a) $\left( 1,2 \right)\cup \left( 2,\infty \right)$,
(b) $\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 3,\infty \right)$,
(c) $\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)$,
(d) $\left( -2,-1 \right)\cup \left( -1,0 \right)\cup \left( 2,\infty \right)$.

Answer 1

Hint: We start solving the problem by recalling about the condition for which the functions $\dfrac{1}{a}$ and ${{\log }_{a}}b$ exist. We find the domain for the functions $\dfrac{1}{4-{{x}^{2}}}$ and $\log \left( {{x}^{3}}-x \right)$ using these conditions. We get two different domains for these functions and we take the intersection of these two intervals to find the common interval which will be our desired domain for the function $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$.

Complete step-by-step answer:
According to the problem, we need to find the domain of the function f which is defined as $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$.
We know that the function $\dfrac{1}{a}$ exists if and only if $a\ne 0$. We use this fact for the function $\dfrac{1}{4-{{x}^{2}}}$.
We have $4-{{x}^{2}}\ne 0$.
$\Rightarrow \left( 2-x \right)\times \left( 2+x \right)\ne 0$.
$\Rightarrow \left( 2-x \right)\ne 0$ and $\left( 2+x \right)\ne 0$.
$\Rightarrow x\ne 2$ and $x\ne -2$.
The function $\dfrac{1}{4-{{x}^{2}}}$ exists in the following interval for x as $R-\left\{ -2,2 \right\}$ ---(1).
We know that the logarithmic function ${{\log }_{a}}b$, for any positive value of a exists if and only if $b>0$. We use this fact for the function $\log \left( {{x}^{3}}-x \right)$.
We have the function $\log \left( {{x}^{3}}-x \right)$ exists if and only if ${{x}^{3}}-x>0$.
\[\Rightarrow x\left( {{x}^{2}}-1 \right)>0\].
\[\Rightarrow x\left( x-1 \right)\left( x+1 \right)>0\] ---(2).
Let us draw the number line and find the feasible interval for x in equation (2).
\[\begin{align}
  & \text{ }\xleftarrow{-ve}\underset{+ve}{\longleftrightarrow}\overset{-ve}{\longleftrightarrow}\xrightarrow[+ve]{} \\
 & \underset{\begin{matrix}
   ' & ' & ' & ' & ' & ' & ' \\
   -\infty & ................ & -1 & 0 & 1 & ................. & \infty \\
\end{matrix}}{\longleftrightarrow} \\
\end{align}\].
From the number line, we can see that the value of equation (2) is negative if the value of x lies between $\left( -\infty ,-1 \right)$ and $\left( 0,1 \right)$. we can also see that the value of equation (2) is positive if the value of x lies between $\left( -1,0 \right)$ and $\left( 1,\infty \right)$.
So, the interval that is suitable for equation (2) is $\left( -1,0 \right)\cup \left( 1,\infty \right)$ ---(3).
Now, we need to find the domain for the function $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$ which will be intersection of the intervals we got in equations (1) and (3).
We know that to find the common interval from two or more intervals, we take the intersection of those intervals.
The required interval for the domain of function $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$ is $\left( \left( -1,0 \right)\cup \left( 1,\infty \right) \right)\cap \left( R-\left\{ -2,2 \right\} \right)$.
Let us draw the number line to check the common interval.
\[\begin{align}
  & \text{ }\xleftarrow{\left( -\infty ,-2 \right)}\text{ }\underset{\text{ }\left( -2,2 \right)\text{ }}{\longleftrightarrow}\text{ }\xrightarrow{\left( 2,\infty \right)} \\
 & \underset{\begin{matrix}
   ' & ' & ' & ' & ' & ' & ' & ' & ' \\
   -\infty & ............. & -2 & -1 & 0 & 1 & 2 & .............. & \infty \\
\end{matrix}}{\longleftrightarrow} \\
 & \text{ }\overset{\left( -1,0 \right)}{\longleftrightarrow}\text{ }\xrightarrow[\left( 1,\infty \right)]{} \\
\end{align}\].

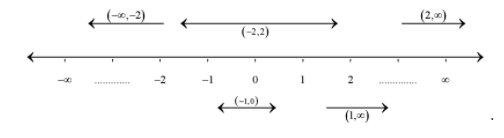
The top part of the number line represents equation (1) and bottom part represents equation (3).
We can see the common interval as $\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)$.
We have found the domain of the function $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$ as $\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)$.
∴ The domain of the function $f\left( x \right)=\dfrac{1}{\left( 4-{{x}^{2}} \right)}\log \left( {{x}^{3}}-x \right)$ is $\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)$.
The correct option for the given problem is (c).

Note: We should not union in place of intersection while finding the common interval as we are checking what is the interval that is present common out of all the intervals we have got. Whenever we get a function that contains multiplication or division of more than one function, we find a domain for individual functions and then take the intersection to find the common interval. Similarly, we can expect problems which contain trigonometric, modulus, step functions while finding the domain.