
Find the distance from origin to the point $\left( 3,4 \right)$.
Answer
600.9k+ views
Hint: Origin is a point of intersection of coordinate axes and coordinates of origin are given as $\left( 0,0 \right)$. Now, find the distance between origin and the given point in the problem using the distance formula, used for calculating distance between two points. It is given as
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Where coordinated of two points are $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left(
{{x}_{2}},{{y}_{2}} \right)$.
Complete step by step answer:
As we know the origin is a point where the axes of the cartesian system intersect each other, other points can then be located with the reference to the origin by giving their numerical coordinates that is the position of their projections along each axis. And the coordinates of origin are given as $\left( 0,0 \right)$.
Now, we have to determine the distance of the point whose coordinates are $\left( 3,4 \right)$ from the origin $\left( 0,0 \right)$. So, we can represent point $\left( 3,4 \right)$ to the coordinate axes as
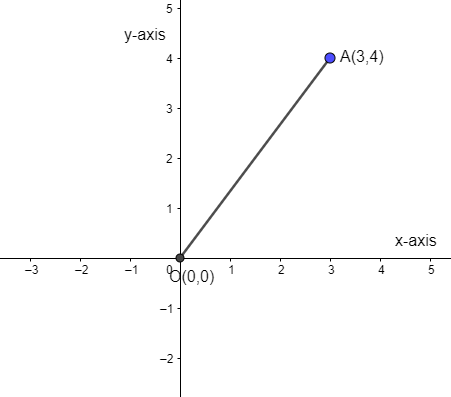
As we know the distance between any two points on the 2-dimensional (x axis and y axis) plane can be given using the distance formula. We can give the distance between the points $P\left( {{x}_{1}},{{y}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}} \right)$ by the distance formula as
PQ $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ ………………………………………(i)
So, we have two points $\left( 3,4 \right)$ and $\left( 0,0 \right)$, where we need to determine the distance between them. So, we can take point $\left( 3,4 \right)$ as $A\left( 3,4 \right)$ and point $\left( 0,0 \right)$ as $O\left( 0,0 \right)$. We can put the values of the coordinates to the expression given in equation (i) to get the distance between both the points i.e. OA.
So, put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 3,4 \right)$
$\Rightarrow {{x}_{1}}=0,{{y}_{1}}=0$ and ${{x}_{2}}=3,{{y}_{2}}=4$.
Hence, we get distance OA as
OA $=\sqrt{{{\left( 0-3 \right)}^{2}}+{{\left( 0-4 \right)}^{2}}}$
OA $=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{9+16}$
OA $=\sqrt{25}=5$
Where squares of the numbers ‘-3’ ad ‘-4’ will be ‘9’ and ‘16’ respectively. And we know the square root of 25 is 5.
Hence, the distance OA or distance between origin and $\left( 3,4 \right)$ is 5.
So, ‘5’ is the correct answer to the given problem.
Note: Another approach for the question would be that we can use Pythagoras theorem to get the distance between origin and $\left( 3,4 \right)$ in following way :-
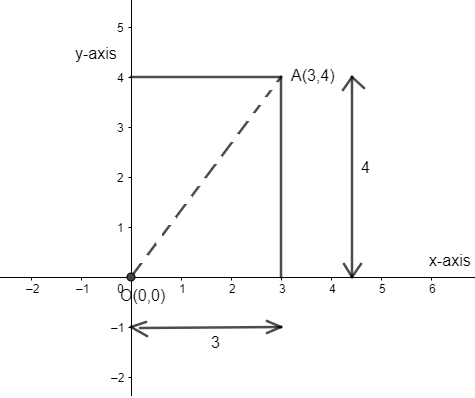
$\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Where coordinated of two points are $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left(
{{x}_{2}},{{y}_{2}} \right)$.
Complete step by step answer:
As we know the origin is a point where the axes of the cartesian system intersect each other, other points can then be located with the reference to the origin by giving their numerical coordinates that is the position of their projections along each axis. And the coordinates of origin are given as $\left( 0,0 \right)$.
Now, we have to determine the distance of the point whose coordinates are $\left( 3,4 \right)$ from the origin $\left( 0,0 \right)$. So, we can represent point $\left( 3,4 \right)$ to the coordinate axes as

As we know the distance between any two points on the 2-dimensional (x axis and y axis) plane can be given using the distance formula. We can give the distance between the points $P\left( {{x}_{1}},{{y}_{1}} \right)$ and $Q\left( {{x}_{2}},{{y}_{2}} \right)$ by the distance formula as
PQ $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ ………………………………………(i)
So, we have two points $\left( 3,4 \right)$ and $\left( 0,0 \right)$, where we need to determine the distance between them. So, we can take point $\left( 3,4 \right)$ as $A\left( 3,4 \right)$ and point $\left( 0,0 \right)$ as $O\left( 0,0 \right)$. We can put the values of the coordinates to the expression given in equation (i) to get the distance between both the points i.e. OA.
So, put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 0,0 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 3,4 \right)$
$\Rightarrow {{x}_{1}}=0,{{y}_{1}}=0$ and ${{x}_{2}}=3,{{y}_{2}}=4$.
Hence, we get distance OA as
OA $=\sqrt{{{\left( 0-3 \right)}^{2}}+{{\left( 0-4 \right)}^{2}}}$
OA $=\sqrt{{{\left( -3 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{9+16}$
OA $=\sqrt{25}=5$
Where squares of the numbers ‘-3’ ad ‘-4’ will be ‘9’ and ‘16’ respectively. And we know the square root of 25 is 5.
Hence, the distance OA or distance between origin and $\left( 3,4 \right)$ is 5.
So, ‘5’ is the correct answer to the given problem.
Note: Another approach for the question would be that we can use Pythagoras theorem to get the distance between origin and $\left( 3,4 \right)$ in following way :-

Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




