Question

Find the distance between two points: (3,4) and (7,7).

Answer 1

Hint: Let us assume two points as: \[\text{A(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{)}\] and \[\text{B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{)}\]. So, distance between both the points is given by the distance formula as: \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]. Now, we have points: (3,4) and (7,7). By using this formula, find the distance between both the points.

Complete step-by-step solution
We have: \[\text{A}\left( 3,4 \right)\] and \[\text{B(}7,7\text{)}\]
Now, we need to find distance between \[\text{A}\left( 3,4 \right)\] and \[\text{B(}7,7\text{)}\]
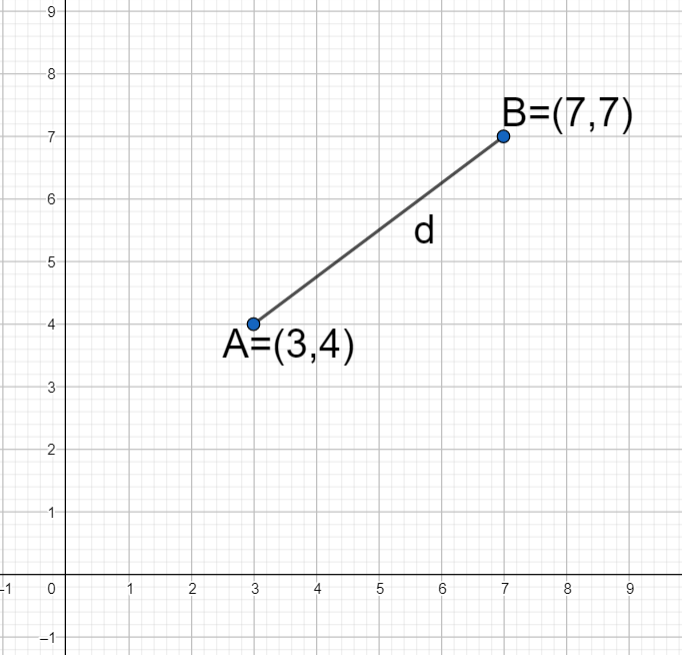
The figure below shows the points as well as the distance between them.

To find distance between two points \[\text{A(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{)}\] and \[\text{B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{)}\] use distance formula, i.e.
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
For the points \[\text{A}\left( 3,4 \right)\] and \[\text{B(}7,7\text{)}\]
\[{{x}_{1}}=3\] and ${{y}_{1}}=4$
\[{{x}_{2}}=7\]and \[{{y}_{2}}=7\]
Therefore, distance between \[\text{A}\left( 3,4 \right)\] and \[\text{B(}7,7\text{)}\] is:
\[\begin{align}
  & d=\sqrt{{{\left( 7-3 \right)}^{2}}+{{\left( 7-4 \right)}^{2}}} \\
 & =\sqrt{16+9} \\
 & =\sqrt{25} \\
 & =5
\end{align}\]
Hence the distance between \[\text{A}\left( 3,4 \right)\] and \[\text{B(}7,7\text{)}\] is 5 units.

Note: The Distance Formula is a useful tool in finding the distance between two points which can be arbitrarily represented as points \[\text{A(}{{\text{x}}_{1}}\text{,}{{\text{y}}_{1}}\text{)}\] and \[\text{B(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{)}\].
The Distance Formula itself is actually derived from the Pythagorean Theorem which is ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$ where c is the longest side of a right triangle (also known as the hypotenuse) and aa and bb are the other shorter sides (known as the legs of a right triangle).
Below is an illustration showing that the Distance Formula is based on the Pythagorean Theorem where the distance d is the hypotenuse of a right triangle.

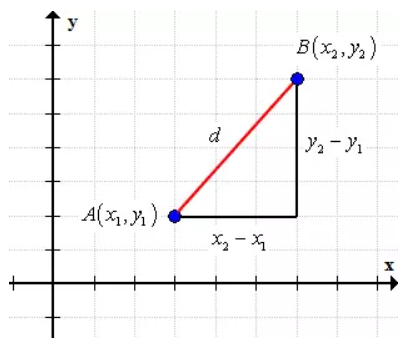
So, by using Pythagoras theorem, we can say that: ${{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}={{d}^{2}}$
Hence, \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
This format always holds true. Given two points, you can always plot them, draw the right triangle, and then find the length of the hypotenuse. The length of the hypotenuse is the distance between the two points.
Don't let the subscripts scare you. They only indicate that there is a "first" point and a "second" point; that is, that you have two points. Whichever one you call "first" or "second" is up to you. The distance will be the same, regardless.