Question

Find the curved surface area and the total surface area of a cone whose:
(1) Base diameter is 28cm and the slant height is 50cm
(2) Base diameter is 70cm and the height is 8.4cm
(a) \[2200c{{m}^{2}},2815c{{m}^{2}};10010c{{m}^{2}},13860c{{m}^{2}}\]
(b) \[2200c{{m}^{2}},2816c{{m}^{2}};10110c{{m}^{2}},13860c{{m}^{2}}\]
(c) \[2200c{{m}^{2}},2816c{{m}^{2}};10010c{{m}^{2}},13860c{{m}^{2}}\]
(d) \[2200c{{m}^{2}},2815c{{m}^{2}};10010c{{m}^{2}},13660c{{m}^{2}}\]
(e) None of these.

Answer 1

Hint: We solve this problem by using the direct formulas for the curved surface area and the total surface area of a cone.

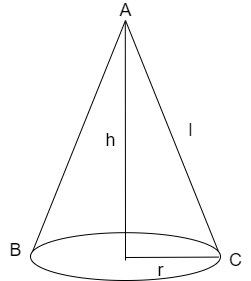
The formula for the curved surface area of a cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow CSA=\pi rl\]
The formula for the total surface area of a cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow TSA=CSA+\pi {{r}^{2}}\]
We also have the relation between the slant height \['l'\], height \['h'\] and base radius \['r'\] that is
\[\Rightarrow {{l}^{2}}={{h}^{2}}+{{r}^{2}}\]

Complete step-by-step solution
We are given two cones and are asked to find the curved surface area and the total surface area.
Let us find the required areas one by one.
Let us take the first cone.
(1) Base diameter is 28cm and the slant height is 50cm
The rough figure of the cone will be

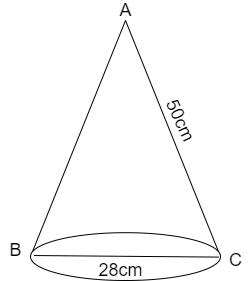
We are given that the slant height is 50cm
Let us assume that the slant height as
\[\Rightarrow l=50cm\]
We are given that the base diameter is 28cm
Let us assume that the base radius as \['r'\]
We know that the base radius of a cone is half of the base diameter.
By using the above result we get the base radius as
\[\Rightarrow r=\dfrac{28cm}{2}=14cm\]
Let us assume that the curved surface area of this cone as \[CSA\]
We know that the formula for the curved surface area of a cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow CSA=\pi rl\]
By using the above formula we get
\[\Rightarrow CSA=\pi \times \left( 14cm \right)\times \left( 50cm \right)\]
We know that the value of \[\pi \] is 3.14.
By substituting the value of \[\pi \] in above equation we get
\[\Rightarrow CSA=2199.11c{{m}^{2}}\simeq 2199c{{m}^{2}}\]
Now, let us assume that the total surface area of the cone as \[TSA\]
 We know that the formula for the total surface area of cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow TSA=CSA+\pi {{r}^{2}}\]
By using the above formula to given cone we get
\[\begin{align}
  & \Rightarrow TSA=2199.11c{{m}^{2}}+\left( \pi \times {{\left( 14cm \right)}^{2}} \right) \\
 & \Rightarrow TSA=2199.11c{{m}^{2}}+615.75c{{m}^{2}} \\
 & \Rightarrow TSA=2814.86c{{m}^{2}}\simeq 2815c{{m}^{2}} \\
\end{align}\]
Now, let us go for the second cone.
(2) Base diameter is 70cm and the height is 8.4cm
The rough figure of the cone will be

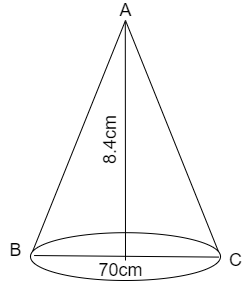
We are given that the height of the cone is 8.4cm
Let us assume that the height of the cone as
\[\Rightarrow h=8.4cm\]
We are given that the base diameter is 70cm
Let us assume that the base radius as \['r'\]
We know that the base radius of a cone is half of the base diameter.
By using the above result we get the base radius as
\[\begin{align}
  & \Rightarrow r=\dfrac{70cm}{2} \\
 & \Rightarrow r=35cm \\
\end{align}\]
Let us assume that the slant height of the cone as \['l'\]
We know that the relation between the slant height \['l'\], height \['h'\] and base radius \['r'\] that is
\[\Rightarrow {{l}^{2}}={{h}^{2}}+{{r}^{2}}\]
By using the above relation we get the length of slant height as
\[\begin{align}
  & \Rightarrow {{l}^{2}}={{\left( 8.4cm \right)}^{2}}+{{\left( 35cm \right)}^{2}} \\
 & \Rightarrow l=\sqrt{70.56+1225} \\
 & \Rightarrow l=35.99\simeq 36cm \\
\end{align}\]
We know that the formula for the curved surface area of cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow CSA=\pi rl\]
By using the above formula we get
\[\Rightarrow CSA=\pi \times \left( 35cm \right)\times \left( 36cm \right)\]
We know that the value of \[\pi \] is 3.14.
By substituting the value of \[\pi \] in above equation we get
\[\Rightarrow CSA=3958.4c{{m}^{2}}\simeq 3958c{{m}^{2}}\]
Now, let us assume that the total surface area of the cone as \[TSA\]
 We know that the formula for the total surface area of cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow TSA=CSA+\pi {{r}^{2}}\]
By using the above formula to given cone we get
\[\begin{align}
  & \Rightarrow TSA=3958.4c{{m}^{2}}+\left( \pi \times {{\left( 35cm \right)}^{2}} \right) \\
 & \Rightarrow TSA=3958.4c{{m}^{2}}+3848.45c{{m}^{2}} \\
 & \Rightarrow TSA=7806.86c{{m}^{2}}\simeq 7807c{{m}^{2}} \\
\end{align}\]
Therefore, the curved surface area and the total surface area of two cones is\[2199c{{m}^{2}},2815c{{m}^{2}};3958c{{m}^{2}},7807c{{m}^{2}}\]
So, option (e) is the correct answer.

Note: Students may make mistakes in the formula of the curved surface area and the total surface area.
We are given the base diameter and the slant height for the first cone.
Now, let us assume that the total surface area of the cone as \[TSA\]
We know that the formula for the curved surface area of a cone having the slant height \['l'\] and the base radius \['r'\] is given as
\[\Rightarrow CSA=\pi rl\]
Here \['l'\] is the slant height not the height of the cone.
Students may do mistake in the slant height and the height and calculate the formula as
\[\Rightarrow CSA=\pi rh\]
This gives the wrong answer.