Question

Find the cube root of 474552.

Answer 1

Hint: Proceed the solution of this question by doing prime factor of given number then try to form triplets of prime numbers, if we get triplets of all prime numbers then it will be a perfect cube and multiplication of all prime numbers will be our cube root.

Complete step-by-step answer:

We know that
The process of cubing is similar to squaring, only that the number is multiplied three times instead of two. The exponent used for cubes is 3. for examples are 8³ = 8*8*8 = 512.

In prime factorisation-
We will find prime factors of 474552, if it is a perfect cube and then will pair them in a group of three.

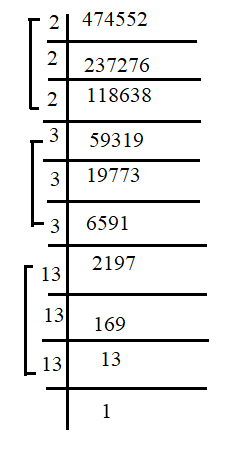
⇒ So, the prime factors of 474552=2×2×2×3×3×3×13×13×13
⇒ 474552 = ${2^3} \times {3^3} \times {13^3}$
Since 2, 3 and 13 occurs in triplets
\[\therefore \]474552 is a perfect cube
On taking cube root on both side
⇒ 474552 = ${2^3} \times {3^3} \times {13^3}$
It can be write like,
 $ \Rightarrow 474552 = {\left( {2 \times 3 \times 13} \right)^3}$
On taking cube root on both side
$ \Rightarrow \sqrt[3]{{474552}} = \sqrt[3]{{{{\left( {2 \times 3 \times 13} \right)}^3}}}$
Cube root can be write raised to power $\dfrac{1}{3}$
\[ \Rightarrow \sqrt[3]{{474552}} = {\left( {2 \times 3 \times 13} \right)^{3 \times \dfrac{1}{3}}}\]

On cancelling exponential power
\[ \Rightarrow \sqrt[3]{{474552}} = {\left( {2 \times 3 \times 13} \right)^1}\]
⇒ So cube root of 474552 ​= 2×3×13=78

Note: We should know that the cubic function is a one-to-one function. This is because cubing a negative number results in an answer different to that of cubing its positive counterpart. We can say this because when three negative numbers are multiplied together, two of the negatives are cancelled but one remains, so the result is also negative. 8³ = 8*8*8 = 512 and (-8) ³ = (-8) *(-8) *(-8) = -512.