Question

Find the cube root of 2744.

Answer 1

Hint: First of all let 2744 = a. To find the cube root of 2744, first of all factorize it and then find the cube root that is \[{{a}^{\dfrac{1}{3}}}\] or \[{{\left( 2744 \right)}^{\dfrac{1}{3}}}\].

Complete step-by-step answer:
Here, we have to find the cube root of 2744.
Before proceeding with this question, we must know what a cube root is.
Cube root of a number is a special value that, when used in a multiplication three times, gives that number. In other words, we can say that the cube root of a number ‘x’ is a number ‘y’ such that \[y\times y\times y=x\] or \[{{y}^{3}}=x\]. Therefore, we get the cube root of x, that is \[y={{x}^{\dfrac{1}{3}}}\].
The graph for \[y={{x}^{\dfrac{1}{3}}}\] can be drawn as

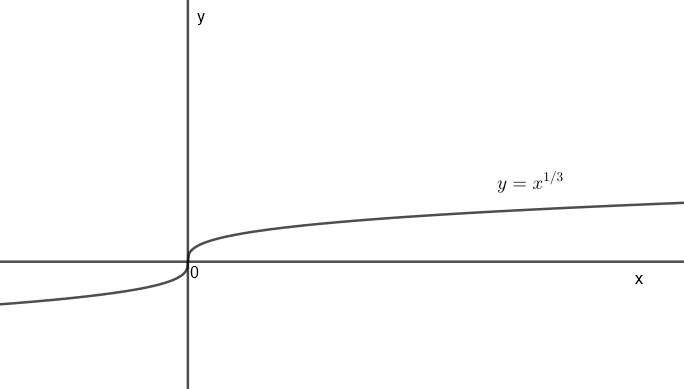
This plot is symmetric with respect to the origin.
Now, here we have to find the cube root of 2744.
Let us take a = 2744.
Therefore, we get the cube root of 2744 as,
\[{{a}^{\dfrac{1}{3}}}={{\left( 2744 \right)}^{\dfrac{1}{3}}}....\left( i \right)\]
First of all, we will resolve 2744 into its factors as follows. Now, we will use the method of factorization, that is,

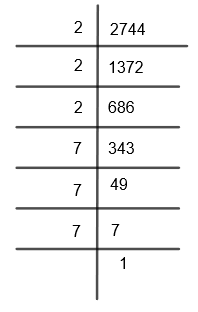
Therefore, we get \[2744=2\times 2\times 2\times 7\times 7\times 7\]
We can also write it as, \[2744={{2}^{3}}{{.7}^{3}}\].
By putting the value of 2744 in equation (i), we get
\[{{a}^{\dfrac{1}{3}}}={{\left( {{2}^{3}}{{.7}^{3}} \right)}^{\dfrac{1}{3}}}\]
 We know that \[{{a}^{n}}.{{b}^{n}}={{\left( ab \right)}^{n}}\].
By applying this in the above equation, we get,
\[{{a}^{\dfrac{1}{3}}}={{\left( {{14}^{3}} \right)}^{\dfrac{1}{3}}}\]
We know that \[{{\left( {{a}^{n}} \right)}^{m}}={{a}^{nm}}\]. By applying this in the above equation, we get,
\[{{a}^{\dfrac{1}{3}}}={{\left( 14 \right)}^{3\times \dfrac{1}{3}}}\]
Therefore, we get \[{{a}^{\dfrac{1}{3}}}=14\]
Hence, we have found that the cube root of 2744 is 14.

Note: Students should properly factorize the given number and cross-check if they are getting the same number by multiplication of factors or not. Also, after finding the cube root, students can take a cube of that cube root to find if it is giving the correct number or not. Students can cross-check in this way.
As we have found that the cube root of 2744 is 14.
We will find \[{{14}^{3}}=14\times 14\times 14\]
We get, \[{{14}^{3}}=2744\]
Therefore, our answer is correct.