Question

Find the correct answer $ A\Delta B= $ \[\]
A. $ \left( A\bigcup B \right)-\left( A\bigcap B \right) $ \[\]
B. $ \left( A\bigcup B \right)+\left( A\bigcap B \right) $ \[\]
C. $ \left( A\bigcap B \right)-\left( A\bigcup B \right) $ \[\]
D. None of these \[\]

Answer 1

Hint: We recall that $ A\Delta B $ represents the symmetric difference of sets which means all the elements which are in either only in set $ A $ or only in set $ B $ but not both sets $ A,B $ that is $ A\Delta B=\left( A-B \right)\bigcup \left( B-A \right) $ . We us the definition of diffr4renc and put $ A-B=A\bigcap {{B}^{'}},B-A={{A}^{'}}\bigcap B $ and then simplify using distributive property $ A\bigcup \left( B\bigcap C \right)=\left( A\bigcup B \right)\bigcap \left( A\bigcap C \right) $ and De-morgan’s law $ {{\left( A\bigcap B \right)}^{'}}={{A}^{'}}\bigcup {{B}^{'}} $ .
 \[\]

Complete step by step answer:
We know that the difference of a set $ A $ from $ B $ represents the elements that are only in $ A $ but not in $ B $ and it is denoted by $ A-B. $ Similarly the difference of a set $ B $ from $ A $ represents the elements that are only in $ B $ but not in $ A $ and it is denoted by $ B-A $ . \[\]

The union of the sets $ A-B $ and $ B-A $ is called symmetric of the sets $ A,B $ and represents all the elements that are wither only in $ A $ or only in $ B $ and is denoted by $ A\Delta B $. Mathematically we have;
\[A\Delta B=\left( A-B \right)\bigcup \left( B-A \right)\]
We know that complement of a set $ A $ can obtain as $ {{A}^{'}}=U-A $ where $ U $ is the universal set.
We know that if we take the intersection of set $ A $ and $ {{B}^{'}} $ from $ A $ and have the elements only in set $ A $ as
\[A-B=A\bigcap {{B}^{'}}\]

Similarly if we take the intersection of set $ {{A}^{'}} $ and $ B $ from $ B $ and have the elements only in set $ B $ as
 \[B-A={{A}^{'}}\bigcap B\]
We put $ A-B,B-A $ in the definition of symmetric difference to have;
\[\begin{align}
  & A\Delta B=\left( A-B \right)\bigcup \left( B-A \right) \\
 & \Rightarrow A\Delta B=\left( A\bigcap {{B}^{'}} \right)\bigcup \left( {{A}^{'}}\bigcap B \right) \\
\end{align}\]
We use the distributive property of sets to have;
\[\begin{align}
  & \Rightarrow A\Delta B=\left( \left( A\bigcap {{B}^{'}} \right)\bigcup {{A}^{'}} \right)\bigcap \left( \left( A\bigcap {{B}^{'}} \right)\bigcup B \right) \\
 & \Rightarrow A\Delta B=\left( \left( A\bigcup {{A}^{'}} \right)\bigcap \left( {{B}^{'}}\bigcup {{A}^{'}} \right) \right)\bigcap \left( \left( A\bigcup B \right)\bigcap \left( {{B}^{'}}\bigcup B \right) \right) \\
\end{align}\]
We use Demorgan’s law and have;
\[\begin{align}
  & \Rightarrow A\Delta B=\left( U\bigcap {{\left( A\bigcap B \right)}^{'}} \right)\bigcap \left( \left( A\bigcup B \right)\bigcap U \right) \\
 & \Rightarrow A\Delta B={{\left( A\bigcap B \right)}^{'}}\bigcap \left( A\bigcup B \right) \\
 & \Rightarrow A\Delta B=\left( A\bigcup B \right)-\left( A\bigcap B \right) \\
\end{align}\]
Hence the correct is option is A and the Venn diagram of $ A\Delta B $ is given below. \[\]

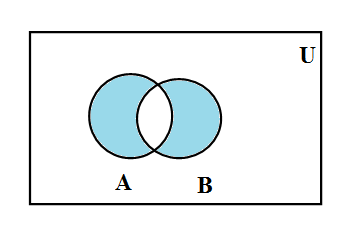
Note:
We note that the union of two sets $ A, B $ represents all the elements that belong to either of the sets $ A $ or $ B $ and is denoted by $ A\bigcup B $ . The intersection of two sets $ A, B $ represents all the elements that belong to both the sets $ A $ and $ B $ and is denoted by $ A\bigcap B $ . Symmetric difference heavily used for indicator function where the function returns 1 or 0 accordingly as output can only belong to two different sets.