Question

Find the coordinates of the points of trisection of the line joining the points (-3,0) and (6,6).

Answer 1

Hint: In order to solve this problem, we need to understand the meaning of trisecting the line. Trisecting is dividing the line into three equal parts. We need to use the section formula to solve this. The section formula says that if the line has endpoints $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ and divides in the ratio m:n starting from point A, then the point C is given by $C\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$.

Complete step-by-step solution:
We have given two points and we need to find the coordinates that trisect the line joining the points (-3,0) and (6,6).
Let’s understand what do we mean by trisection.
We need to divide the line joining AB into three equal parts.
This can be done by considering the ratio 2:1 for the first point and then by the ratio 1:2.
We can understand with the help of a diagram better.

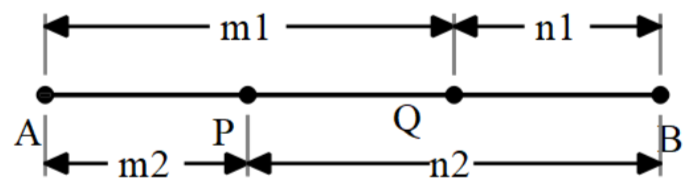
From this diagram, we can see that to get point Q we need to divide the line in the ratio ${{m}_{1}}:{{n}_{1}}$ and to get the point P we need to divide the point in the ratio ${{m}_{2}}:{{n}_{2}}$.
As all the parts are of the same length, we can write that ${{m}_{1}}:{{n}_{1}}=2:1$ and ${{m}_{2}}:{{n}_{2}}=1:2$ .
We need to divide the length with the help of the section formula.
The section formula says that if the line has endpoints $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ and divides in the ratio m:n starting from point A, then the point C is given by $C\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$
So, using this formula lets first calculate the coordinates of point P
For point P, $A\left( {{x}_{1}},{{y}_{1}} \right)=A\left( -3,0 \right),B\left( {{x}_{2}},{{y}_{2}} \right)=B\left( 6,6 \right)$ and the ratio is 2:1
Using the formula, we get,
$P\left( \dfrac{2\times 6+1\times -3}{2+1},\dfrac{2\times 6+1\times 0}{2+1} \right)$
Solving this we get,
$\begin{align}
  & P\left( \dfrac{12-3}{3},\dfrac{12}{3} \right) \\
 & P\left( 3,4 \right) \\
\end{align}$
We know the first coordinate. Let find the second coordinate that is Q.
For point Q, $A\left( {{x}_{1}},{{y}_{1}} \right)=A\left( -3,0 \right),B\left( {{x}_{2}},{{y}_{2}} \right)=B\left( 6,6 \right)$ and the ratio is 1:2
Using the formula, we get,
$Q\left( \dfrac{1\times 6+2\times -3}{1+2},\dfrac{1\times 6+2\times 0}{1+2} \right)$
Solving this we get,
$\begin{align}
  & Q\left( \dfrac{6-6}{3},\dfrac{6}{3} \right) \\
 & Q\left( 0,2 \right) \\
\end{align}$
Therefore, the two points are P (3,4) and Q (0,2).

Note: In this problem, it is very important from where we start ratio m:n, because as the point is not symmetric the equation may change and the P and Q might interchange. Further, to cross-check can always plot all the points again and check the answer.