Question

Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX plane.

Answer 1

Hint-Here we will proceed by using the equation of line passing through points i.e. $\dfrac{{x - {x_1}}}{{{x_2} - {x_1}}} = \dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{z - {z_1}}}{{{z_2} - {z_1}}}$to find the line. Then we will equate this equation of line with a constant such that we will get the value of constant. Hence we will use the value of constant to get the required coordinates of the point.

Complete Step-by-Step solution:

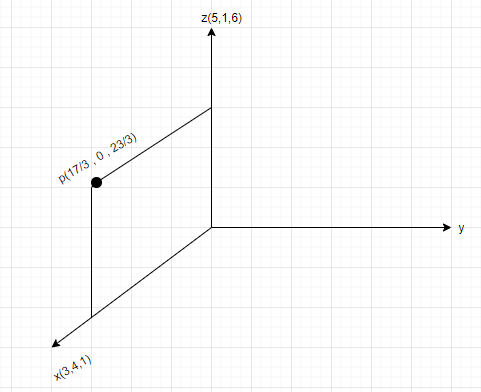
Let z(5,1,6) and x(3,4,1) be the points from where the line crosses the ZX plane.
We know that the equation of the line that passes through the points z$\left( {{x_1},{y_1},{z_1}} \right)$ and x$\left( {{x_2},{y_2},{z_2}} \right)$ is given by the relation-
$\dfrac{{x - {x_1}}}{{{x_2} - {x_1}}} = \dfrac{{y - {y_1}}}{{{y_2} - {y_1}}} = \dfrac{{z - {z_1}}}{{{z_2} - {z_1}}}$
So using the given points z(5, 1, 6) and x(3, 4, 1),
Where $
  {x_1} = 5,{y_1} = 1,{z_1} = 6 \\
  {x_2} = 3,{y_2} = 4,{z_2} = 1 \\
 $
We will find the line –
$\dfrac{{x - 5}}{{ - 2}} = \dfrac{{y - 1}}{3} = \dfrac{{z - 6}}{{ - 5}}$
Now let $\dfrac{{x - 5}}{{ - 2}} = \dfrac{{y - 1}}{3} = \dfrac{{z - 6}}{{ - 5}}$=k
Which implies that x = 5 – 2k, y = 3k + 1, z = 6 – 5k
And any point on the line is of the form (5 – 2k, 3k + 1, 6 – 5k).
So, the equation of ZX plane is y = 0(by using standard equation of plane parallel to ZX)
Since the line passes through YZ – plane,
Then we have,
3k + 1 = 0,
Which implies that $k = - \dfrac{1}{3}$
Now put the value of k to find x and z,
$x = 5 - 2k = 5 - 2\left( { - \dfrac{1}{3}} \right)$
$x = \dfrac{{17}}{3}$
$z = 6 - 5k = 6 - 5\left( {\dfrac{{ - 1}}{3}} \right)$
$z = \dfrac{{23}}{3}$
So the required point is $\left( {\dfrac{{17}}{3},0,\dfrac{{23}}{3}} \right)$
Note – Here in order to solve this question, we can also use another way i.e. vector concept which implies that we will use vectors to locate the positions of the coordinates. Also while solving this question, many of us skip the step of constant and directly substitute the values of given coordinates into the formula but this mistake will lead to undefined answers as we will not get the proper coordinates of the required point.