Question

Find the coordinates of the point on the parabola ${{\text{y}}^2} = 8{\text{x}}$ whose focal distance is $8$.

Answer 1

Hint: From the question, we have to find the coordinate points from the given information. First, we are going to know the terms used in the parabola and while comparing that with the given to find some results then doing some deep calculations for finding the points.
The locus of a point whose distance from a fixed point is equal to its distance from a fixed line is called a parabola. That is a parabola is conic whose eccentricity is $1$.

Formula used:

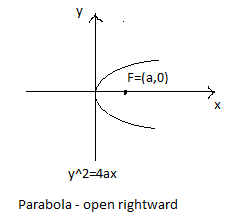
The standard equation of the parabola is${{\text{y}}^2} = 4{\text{ax}}$ .
The distance between the two points are given by\[{\text{d}} = \sqrt {{{\left( {{\text{x}} - {{\text{x}}_{\text{1}}}} \right)}^2} + {{\left( {{\text{y}} - {{\text{y}}_{\text{1}}}} \right)}^2}} \].
We know that${\left( {{\text{a}} + {\text{b}}} \right)^2} = {{\text{a}}^2} + 2{\text{ab}} + {{\text{b}}^2}$ .

Complete step-by-step solution:
By the given, the parabola is open rightward.
Let the coordinates of the point be ${\text{P}}\left( {{\text{x,y}}} \right)$.
By comparing, the standard equation of the parabola ${{\text{y}}^2} = 4{\text{ax}}$to the given parabolic equation${{\text{y}}^2} = 8{\text{x}}$. Then, we get the focal length ${\text{a}}$.
${{\text{y}}^2} = 8{\text{x}}$
$ \Rightarrow {{\text{y}}^2} = 4\left( 2 \right){\text{x}}$
$ \Rightarrow {{\text{y}}^2} = 4\left( {\text{a}} \right){\text{x}}$
Therefore, the focal length is${\text{a}} = 2$.
Thus, the focus of the parabola be $\left( {{\text{F}}\left( {{\text{a}},0} \right) = } \right)$${\text{F}}\left( {2,0} \right)$.
Here, consider the focus points as $\left( {{{\text{x}}_{\text{1}}}{\text{,}}{{\text{y}}_{\text{1}}}} \right)$=$\left( {2,0} \right)$.
Now, we move to find the coordinate points by using the above information.
We have the focal distance is $8$ from the given. Now, we substitute focal distance and focus on the distance formula to find the points.
\[{\text{d}} = \sqrt {{{\left( {{\text{x}} - {{\text{x}}_{\text{1}}}} \right)}^2} + {{\left( {{\text{y}} - {{\text{y}}_{\text{1}}}} \right)}^2}} \]
$ \Rightarrow 8 = \sqrt {{{\left( {{\text{x}} - 2} \right)}^2} + {{\left( {{\text{y}} - 0} \right)}^2}} $
By squaring on both sides. We get,
\[ \Rightarrow {\left( 8 \right)^2} = {\left( {\sqrt {{{\left( {{\text{x}} - 2} \right)}^2} + {{\left( {{\text{y}} - 0} \right)}^2}} } \right)^2}\]
\[ \Rightarrow 64 = {\left( {{\text{x}} - 2} \right)^2} + {\left( {{\text{y}} - 0} \right)^2}\]
Expand the square term on right hand side (RHS). Then, we get
$ \Rightarrow \left( {{{\text{x}}^2} - 4{\text{x}} + 4} \right) + {{\text{y}}^{\text{2}}} = 64$
$ \Rightarrow \left( {{{\text{x}}^2} - 4{\text{x}} + 4} \right) + 8{\text{x}} = 64$
$ \Rightarrow {{\text{x}}^2} + 4{\text{x}} + 4 = 64$
Arrange the above equation to one side. Then, we get
$ \Rightarrow {{\text{x}}^2} + 4{\text{x}} + 4 - 64 = 0$
$ \Rightarrow {{\text{x}}^2} + 4{\text{x}} - 60 = 0$
Now, use the factorization method to find the required point.
$ \Rightarrow \left( {{\text{x}} + 10} \right)\left( {{\text{x}} - 6} \right) = 0$
Equate the above both terms are equal to zero. Then, we get the required point.
$ \Rightarrow \left( {{\text{x}} + 10} \right) = 0$or$\left( {{\text{x}} - 6} \right) = 0$.
$ \Rightarrow {\text{x}} = - 10$ or ${\text{x}} = + 6$
By the given parabola, ${\text{x}}$ cannot be negative in this problem. So,${\text{x}} = 6$ be the required point.
Therefore, the required points can be found by the following steps.
Now, substitute ${\text{x}} = 6$ in the given equation of the parabola be ${{\text{y}}^2} = 4\left( 2 \right){\text{x}}$ . Then, we get
$ \Rightarrow {{\text{y}}^2} = 4\left( 2 \right)\left( 6 \right)$
$ \Rightarrow {{\text{y}}^2} = 48$
Taking square root on both sides. We get
$ \Rightarrow \sqrt {{{\text{y}}^2}} = \sqrt {48} $
$ \Rightarrow {\text{y}} = \sqrt {4 \times 3 \times 4} $
\[ \Rightarrow {\text{y}} = \pm 4\sqrt 3 \] .

Therefore, the coordinate points are $\left( {6,4\sqrt 3 } \right)$ and $\left( {6, - 4\sqrt 3 } \right)$.

Note: We have to know that, the axis of the parabola ${{\text{y}}^2} = 4{\text{ax}}$ is positive $x - $axis (assuming${\text{a}} > 0$) or ${\text{y = 0}}$. The fixed point used to draw the parabola is called the focus. The focus of the parabola be ${\text{F}}\left( {{\text{a}},0} \right)$. The focal distance is the distance between a point on the parabola and its focus. The focal length of a parabola is ${\text{a}}$.