Question

Find the coordinates of the centroid of the triangle, whose sides are $12{{x}^{2}}-20xy+7{{y}^{2}}=0$ and $2x-3y+4=0$?

Answer 1

Hint: We start solving the problem by drawing the given information and recalling the fact that the pair of straight lines of equation $a{{x}^{2}}+bxy+c{{y}^{2}}=0$ intersects at $\left( 0,0 \right)$ to get our first vertex of triangle. We then find equation of both lines present in the pair of straight lines $12{{x}^{2}}-20xy+7{{y}^{2}}=0$ and find the point of intersection these lines with the line $2x-3y+4=0$ to get the remaining two vertices of triangle. We then use the fact that the centroid of the triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$ to find the coordinates of the required centroid.

Complete step-by-step solution
According to the problem, we need to find the coordinates of the centroid of the triangle, whose sides are $12{{x}^{2}}-20xy+7{{y}^{2}}=0$ and $2x-3y+4=0$.
Let us draw the given information to get a better view.

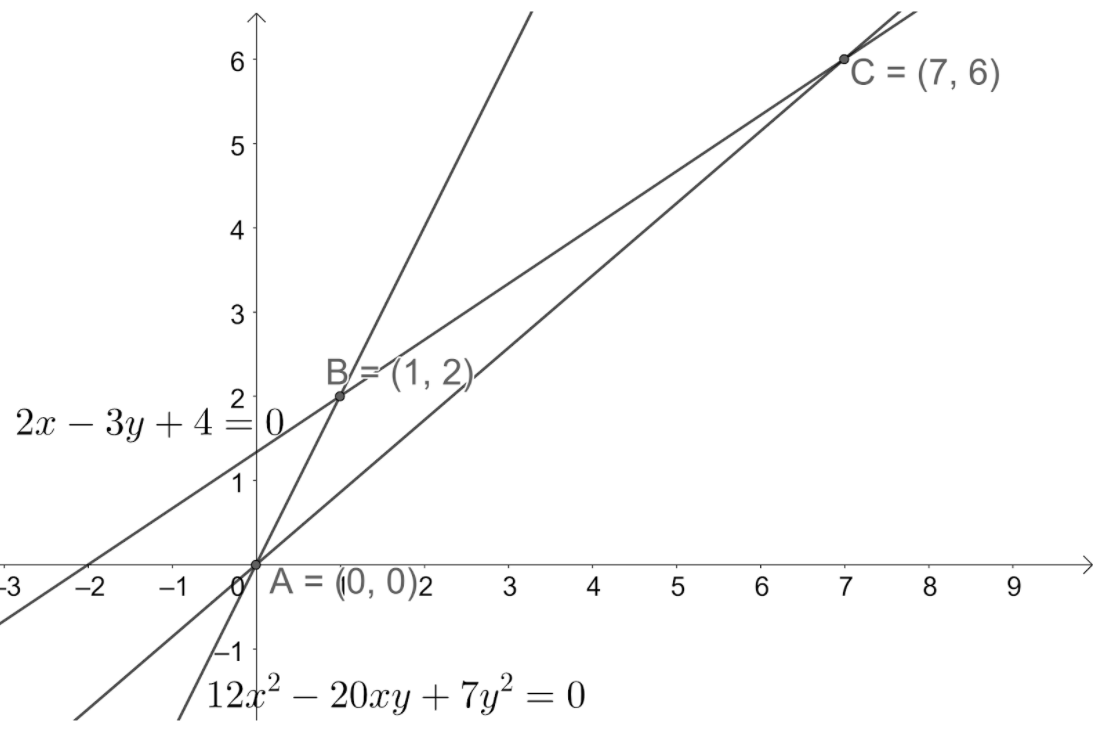
We know that the pair of straight lines of equation $a{{x}^{2}}+bxy+c{{y}^{2}}=0$ intersects at $\left( 0,0 \right)$. So, we get one of the vertices of the triangles as $A\left( 0,0 \right)$ ---(1).
Let us now, find the intersection points of the line $2x-3y+4=0$ with pair of straight lines $12{{x}^{2}}-20xy+7{{y}^{2}}=0$.
Let us first find the equations of both the straight lines present in $12{{x}^{2}}-20xy+7{{y}^{2}}=0$.
So, we get $12{{x}^{2}}-6xy-14xy+7{{y}^{2}}=0$.
$\Rightarrow 6x\left( 2x-y \right)-7y\left( 2x-y \right)=0$.
$\Rightarrow \left( 6x-7y \right)\left( 2x-y \right)=0$.
$\Rightarrow \left( 6x-7y \right)=0$ and $y=2x$.
$\Rightarrow y=\dfrac{6x}{7}$ and $y=2x$ ---(2).
Let us substitute the $y=2x$ in the line $2x-3y+4=0$.
$\Rightarrow 2x-3\left( 2x \right)+4=0$.
$\Rightarrow 2x-6x+4=0$.
$\Rightarrow -4x+4=0$.
$\Rightarrow 4x=4$.
$\Rightarrow x=1$. Let us substitute this in the equation of line $y=2x$ to get y-coordinate.
So, we get $y=2\left( 1 \right)=2$.
We have got the other vertex of the triangle as $B\left( 1,2 \right)$ ---(2).
Let us substitute the $y=\dfrac{6x}{7}$ in the line $2x-3y+4=0$.
$\Rightarrow 2x-3\left( \dfrac{6x}{7} \right)+4=0$.
$\Rightarrow 2x-\dfrac{18x}{7}+4=0$.
$\Rightarrow \dfrac{14x-18x+28}{7}=0$.
$\Rightarrow -4x+28=0$.
$\Rightarrow 4x=28$.
$\Rightarrow x=7$. Let us substitute this in the equation of line $y=\dfrac{6x}{7}$ to get y-coordinate.
So, we get $y=\dfrac{6\left( 7 \right)}{7}=6$.
We have got the other vertex of the triangle as $C\left( 7,6 \right)$ ---(3).
So, we have found the vertices of the triangle as $A\left( 0,0 \right)$, $B\left( 1,2 \right)$ and $C\left( 7,6 \right)$.
We know that the centroid of the triangle with vertices $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
So, the centroid of triangle ABC is $\left( \dfrac{0+1+7}{3},\dfrac{2+6+0}{3} \right)=\left( \dfrac{8}{3},\dfrac{8}{3} \right)$.
$\therefore$ The coordinates of the centroid of the triangle, whose sides are $12{{x}^{2}}-20xy+7{{y}^{2}}=0$ and $2x-3y+4=0$ is $\left( \dfrac{8}{3},\dfrac{8}{3} \right)$.

Note: We can solve this problem by finding all the medians of the triangle and finding the point of intersection of them to get the centroid. We should know that the equation $a{{x}^{2}}+bxy+c{{y}^{2}}=0$ always represents the pair of straight lines unless it is mentioned in the problem. We can also find the area of the triangle after finding each vertex of this triangle. Similarly, we expect problems to find the circum-center, area of the triangle by giving the equation of the sides of the triangle.