Question

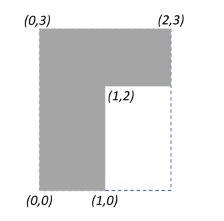
Find the coordinates of centre of mass of the lamina shown in the figure:

A. (0.75, 1.75)
B. (0.75, 1.5)
C. (0.5, 1.75)
D. (0.5, 1.5)

Answer 1

Hint: Since it is not essentially a straightforward calculation for the position of the centre of mass for a structure such as a lamina, think of how you could divide the lamina into two different parts for which the calculation will be much easier. In other words, divide the lamina into two rectangles and locate each of their centroids. To this end, find the position of the effective centre of mass for the lamina altogether. Remember that the centre of mass is basically the average position of all parts of the laminar system.

Formula used:
Surface density $\sigma = \dfrac{m}{A}$, where m is the mass of the object and A is the surface are of the object.
The coordinates of the effective centre of mass of a system in terms of the centre of mass of its discrete components (here, for two parts A and B of the system):
$CoM_{effective}= \left(X_{CoM},Y_{CoM}\right)$
$X_{CoM} = \dfrac{m_Ax_A + m_Bx_B}{m_A+m_B}$ and $Y_{CoM} = \dfrac{m_Ay_A + m_By_B}{m_A+m_B}$, where m denotes mass, and x and y denote the coordinates of the CoM in the discrete parts.

Complete answer:
Let us first look at some terms for a better understanding of what is asked from us.
We have an inverted L-shaped lamina whose centre of mass coordinates we’re supposed to find.
The centre of mass of a system is defined at the point at which the whole mass of the system appears to be concentrated. Any external force applied acts on this point. In case of a rigid body, the centre of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid.
Let us begin by dividing our lamina in such a way that we get two rectangles A and B.
Let $m_A$ and $area_A$ be the mass and area of rectangle A, and $m_B$ and $area_B$ be the mass and area of rectangle B

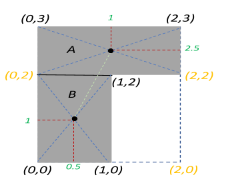
Assuming that the lamina is of uniform surface density $\sigma$ throughout,
$\Rightarrow \sigma_A = \sigma_B \Rightarrow \dfrac{m_A}{area_A} = \dfrac{m_B}{area_B} \Rightarrow \dfrac{m_A}{2 \times 1} = \dfrac{m_B}{1 \times 2} \Rightarrow m_A = m_B =$ say $m$

Now, we know that the centroid of a rectangle, which is the point of intersection of its diagonals, will be the centre of mass of the rectangle. We can determine the coordinates of the centroid by drawing a horizontal and a vertical line from the centroid that meets the length and breadth of the rectangle (see figure).

The centroid of rectangle A is found to be at $CoM_A = (1,2.5)$, and the centroid of rectangle B is found to be at $CoM_B = (0.5,1)$. Therefore, the centre of mass of the entire lamina lies somewhere on the line joining these two points.

We can find the coordinates of the resultant centre of mass for the entire lamina by putting together the centre of mass components that we got from dividing the lamina into two rectangles.

This is given by:
$CoM_{lamina}= \left(X_{CoM},Y_{CoM}\right)$
$X_{CoM} = \dfrac{m_Ax_A + m_Bx_B}{m_A+m_B}$ and $Y_{CoM} = \dfrac{m_Ay_A + m_By_B}{m_A+m_B}$
But we have deduced that $m_A = m_B = m$

$\Rightarrow X_{CoM} = \dfrac{m(x_A +x_B)}{m(2)} = \dfrac{x_A+x_B}{2} = \dfrac{1+0.5}{2} = 0.75$ and,
$ Y_{CoM} = \dfrac{m(y_A +y_B)}{m(2)} = \dfrac{y_A+y_B}{2} = \dfrac{2.5+1}{2} = 1.75$
Therefore, the coordinates of the centre of mass of the lamina will be
$CoM_{lamina}= \left(X_{CoM},Y_{CoM}\right) = \left(0.75, 1.75\right)$

So, the correct answer is “Option A”.

Note:
Remember that here, we treat the lamina to be a rigid body with a uniform surface density. This means that the distance between any two points on the lamina remains constant regardless of external forces acting on it. It is hence immune to any deformations and this means that the surface density remains uniform throughout the rigid body surface.
It is also important to understand the distinction between centre of mass and centre of gravity. Centre of mass, as we have defined earlier, is the point at which the distribution of mass is equal in all directions whereas centre of gravity is the point at which the distribution of weight is equal in all directions. Centre of mass arises from the geometric behaviour of the object and hence does not depend on the gravitational field whereas centre of gravity arises from the physical behaviour of the object and depends on the gravitational field acting on it.
However, if all particles on a rigid body experience the same acceleration due to gravity, i.e., when the gravitational field is uniform throughout all points in the entire object, then the centre of mass coincides with the centre of gravity.