Question

How do you find the conjugate of the complex number $7-3i$ ?

Answer 1

Hint: We are given a complex number as $7-3i$ , we are asked to find the conjugate of it, to find the conjugate of our given number we will learn what are complex number, how they are defined, we learn about ‘I’, then we will understand about conjugate, work on some example. Once we get the concept we work on $7-3i$ .

Complete step-by-step answer:
We are given a number as $7-3i$ , we are asked to find the conjugate of it, to do so we will first learn about complex numbers.
Complex numbers are defined by $z=a+ib$ , where a, b are real numbers, and ‘I’ is called iota.
‘I’ is used to denote the square root of -1 i.e. $i=\sqrt{-1}$ .
Now, we will learn about the conjugate,
The conjugate of any complex number ‘z’ is denoted by $\overline{z}$ and the conjugate of any complex number is the reflection of it along the real axis (x-axis).
And to find the conjugate of a number, we just need to find a number whose real part is the same as the given complex number and the imaginary part is opposite is sign but same in magnitude as the given complex number.

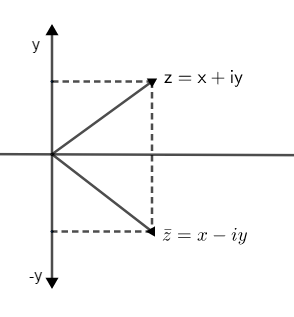
So, for any complex number $2=x+iy$ , its conjugate have real part is same as real part of ‘z’ which is ‘x’ while imaginary part is opposite in sign than that of ‘z’, so its imaginary part is ‘-y’,
So, the conjugate of $z=x+iy$ is $\overline{z}=x-iy$ .
For example we have $z=2+3i$ then the conjugate of it is $\overline{z}=2-3i$.
Now we work on our problem.
We have $z=7-3i$ , here $x=7$ and $y=-3$ .
So, its conjugate is $\overline{z}=x-iy$ .
So putting value, we get –
$\begin{align}
  & \overline{z}=7-\left( -3 \right)i \\
 & =7+3i \\
\end{align}$
So, the conjugate of $7-3i$ is $7+3i$ .

Note: Remember that it is not that we just need to change the positive to negative always in the imaginary part in actual, the sign gets reversed positive becomes negative but also negative becomes positive.
Also we do not have to change sign of whole the term that is for $z=2+3i$ , its conjugate is not $\overline{z}=-2-3i$ ,
Remember magnitude of any real quantity means the absolute value of it, for -2 and 2, their magnitude is same as $\left| -2 \right|=2$ and $\left| 2 \right|=2$ .