Question

Find the circumference of a wheel whose diameter is 126cm. Find the distance covered by it by taking 50 rounds in meters.

Answer 1

Hint: Note that, the circumference of a circle having radius r is $2\pi r$units.
Use this to find the circumference of the given wheel.
Now, if the wheel takes one round, it covers a distance equal to its circumference. Therefore, in taking 50 rounds, the total distance covered by the wheel will be $50 \times $circumferences.

Complete step-by-step answer:
Given, the diameter of the wheel is 126cm.

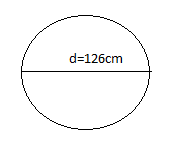
The radius is $\dfrac{{diameter}}{2} = \dfrac{{126cm}}{2} = 63cm$.
We know, the circumference of a circle having radius r is $2\pi r$units.
⇒ The circumference of the wheel is
$ = 2\pi \times \left( {63} \right)cm$
On substituting the value of $\pi = \dfrac{{22}}{7}$, we get,
$ = 2 \times \dfrac{{22}}{7} \times \left( {63} \right)cm$
On simplification we get,
${\text{ = 396cm}}$
So, the circumference of the wheel is 396cm
Now, if the wheel takes one round, it covers a distance equal to its circumference, i.e. 396 cm.
Therefore, in taking 50 rounds, the total distance covered by the wheel will be
${{ = 396 \times 50cm}}$
On multiplying we get,
${{ = 1980cm}}$
Now as $1m = 100cm$,
We get,
${\text{ = 19}}{\text{.80m}}$
∴ In taking 50 rounds, the total distance covered by the wheel will be 19.80 meter.

Note: The circumference of a circle having radius r is $2\pi r$ units. The area for the same is given by $\pi {r^2}$ square units.
Here we were given to find the distance covered in the number of turns of a wheel, so we must consider the circumference of the circle, as the wheel rotates on its outline and that will give the distance covered.
Here we were given the diameter, in different problems we can be given the circumference so we can easily multiply it with the number of turns to get the distance covered.