Question

Find the circumcircle of the triangle formed by the lines $x = 0$ , $x + y + 3 = 0$ and $x - y + 1 = 0$

Answer 1

Hint: In order to find the circumcircle of the triangle formed by the given lines, first we will discuss the nature of triangle formed on the basis of the slopes of the given lines and further on the basis of the triangle formed, we will discuss the nature of the circle and also the equation of the circle.

Complete step-by-step answer:

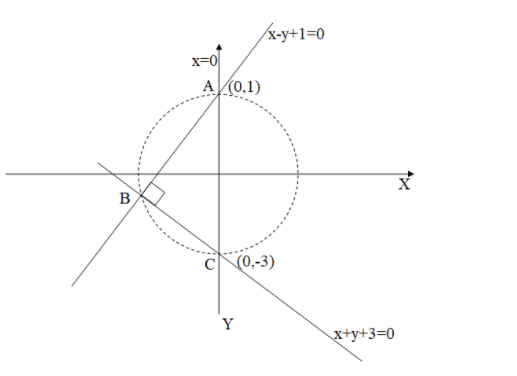
We have equation of three lines they are:
$x = 0$ , $x + y + 3 = 0$ and $x - y + 1 = 0$
Let us first find the slope of the lines except the y axis line.
Slope of $x - y + 1 = 0$ is 1
Slope of $x + y + 3 = 0$ is -1.
As we know that if the product of the slopes of the line is -1, then the lines are perpendicular to each other.
Also from the above observation, we can see that the product of the slopes of the lines is -1. So, we can conclude that the lines are perpendicular to each other.
On the basis of our observation of one of the angles of the triangle, we can conclude that the triangle is a right angled triangle.
We can observe the same as we see the diagram according to the question.
As we have found out that the line AC is the hypotenuse of the triangle formed, so the line AC will act as the diameter for the circumcircle formed by these lines.
Now as we have the diameter, we can easily find out the equation of the circle formed by the help of coordinates of the diameter of the circle.
In order to find the coordinates of the diameter, let us solve the equations of the lines by substitution to find the coordinates of the point A and C.
For the coordinates of the point A, let us solve the equation $x = 0$ and $x - y + 1 = 0$ .
$
  x = 0\& x - y + 1 = 0 \\
   \Rightarrow 0 - y + 1 = 0 \\
   \Rightarrow y = 1 \\
   \Rightarrow A = \left( {0,1} \right) \\
 $
For the coordinates of the point C, let us solve the equation $x = 0$ and $x + y + 3 = 0$ .
$
  x = 0\& x + y + 3 = 0 \\
   \Rightarrow 0 + y + 3 = 0 \\
   \Rightarrow y = - 3 \\
   \Rightarrow C = \left( {0, - 3} \right) \\
 $
As, now we have the coordinates of the diameter, so let us find out the equation of the circumcircle.
Therefore, the equation of the circle is:
$
  \because \left( {x - {x_1}} \right)\left( {x - {x_2}} \right) + \left( {y - {y_1}} \right)\left( {y - {y_2}} \right) = 0 \\
   \Rightarrow \left( {x - 0} \right)\left( {x - 0} \right) + \left( {y - 1} \right)\left( {y - \left( { - 3} \right)} \right) = 0 \\
   \Rightarrow {x^2} + {y^2} - y + 3y - 3 = 0 \\
   \Rightarrow {x^2} + {y^2} + 2y - 3 = 0 \\
 $
Hence, the equation of the circumcircle is ${x^2} + {y^2} + 2y - 3 = 0$

Note: Circumcircle is the circle formed by the points joining some figures and the circle lies on the outer side of the points, whereas the incircle is the circle formed on the inner side of the figure made by some points. There is no direct method or formula to find the equation of the circumcircle, so students must first find some points or some diameter to find the equation of the circle. This problem can also be solved by directly finding three points by solving the equation and then finding the constant terms in the general formula of the circle.