Question

Find the charge that flows from point $A$ to $B$, when the switch is closed.

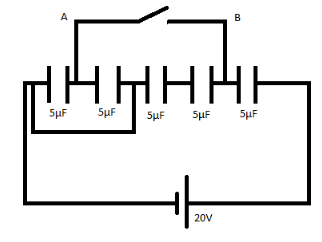
Answer 1

Hint: A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals. The effect of a capacitor is known as capacitance. The resistance of an ideal capacitor is zero. The reactance of an ideal capacitor, and therefore its impedance, is negative for all frequency and capacitance value. To solve this problem we should try to turn a complex capacitor system into a simple one. We should know how to calculate effective capacitances of a system.

Complete step by step answer:
Rearranging the circuit

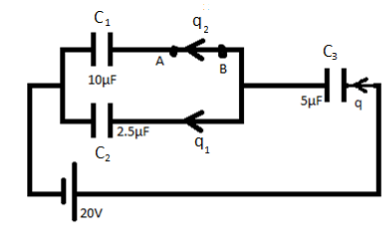
$q = CV$
Equivalent capacitance of the circuit is
${C_1}\,and\,{C_2}$ are in parallel
So
${C_T} = {C_1} + {C_2}$
Put the value
${C_T} = 10 + 2.5$
$\Rightarrow {C_T} = 12.5\mu F$
${C_T}\,and\,{C_3}$ are in series
${C_{eq}} = \dfrac{{{C_3} \times {C_T}}}{{{C_3} + {C_T}}}$
Put the value
${C_{eq}} = \dfrac{{5 \times 12.5}}{{12.5 + 5}}$
\[\Rightarrow {C_{eq}} = \dfrac{{25}}{7}\mu F\]
As we know that
$q = CV$

Put the value
$q = \dfrac{{25}}{7} \times 20$
$\Rightarrow q = \dfrac{{500}}{7}\mu F$
Now apply Kirchhoff’s Voltage Law
It states that “the algebraic sum of all voltage difference is equal to zero.”
$\sum\limits_{}^{} V = 0$
$ \Rightarrow 20 = \dfrac{{20 \times 25}}{{7 \times 5}} + \dfrac{{{q_1}}}{{2.5}}$
$ \Rightarrow {q_1} = \dfrac{{100}}{7}\mu F$
Charge flow from $B$ to $A$
$ \Rightarrow {q_2} = \dfrac{{400}}{7}\mu F$
Charge flow from A to B
$ \therefore {q_2} = - \dfrac{{400}}{7}\mu F$

Hence, the charge that flows from point $A$ to $B$ is $- \dfrac{{400}}{7}\,\mu F$.

Note: In a simple plate capacitor, a voltage applied between two conductive plates creates a uniform electric field between those plates. The electric field strength in a capacitor is directly proportional to the voltage applied and inversely proportional to the distance between the plates. The energy stored in a capacitor can be expressed in three ways, energy in joules, charge is in coulombs, and capacitance in farads.