
Find the centre of mass of three particles at the vertices of an equilateral triangle. The masses of the particles are 100g, 150g and 200g respectively. Each side of the equilateral triangle is 0.5m long.
Answer
535.8k+ views
Hint: First we need to define the coordinates for the given masses. The centre of mass of the system of given masses can be calculated by taking the ratio of sum of products of the masses and their distances from the origin to the sum of the given masses.
Formula used:
The centre of mass of a system of mass can be given as
$C = \dfrac{{\sum {{m_i}r_i^2} }}{{\sum {{m_i}} }}$
Here ${m_i}$ represents the mass of the ith particle while ${r_i}$ represents the distance of the ith mass from the origin.
Detailed step by step solution:
The centre of mass of a system of masses is defined as the point on a body about which the whole mass of the given system is concentrated. Mathematically, it is equal to the ratio of sum of products of the masses and their distances from the origin to the sum of the given masses.
We are given three particles whose masses are given as
$\begin{array}{l}
{m_1} = 100g\\
{m_2} = 150g\\
{m_3} = 200g
\end{array}$
These three particles are arranged on the vertices of an equilateral triangle. Each side of the equilateral triangle has length of 0.5 m. We can draw the following diagram for this arrangement.
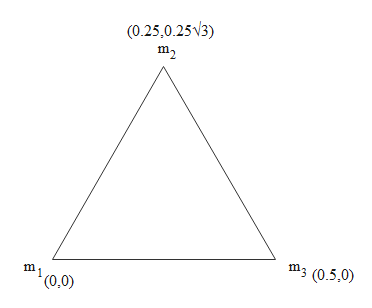
Now based on this diagram, we have three masses and their coordinates. Now we can find the coordinates of the centre of mass by using the formula given in equation (i). First, let us calculate the x-coordinate of the centre of mass. For this we will use the x-coordinates of the given masses. This is done in the following way.
$\begin{array}{l}
\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)\\
\left( {{x_2},{y_2}} \right) = \left( {0.5,0} \right)\\
\left( {{x_3},{y_3}} \right) = \left( {0.25,0.25\sqrt 3 } \right)\\
{x_{CM}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\
= \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0.5} \right) + \left( {200 \times 0.25} \right)}}{{\left( {100 + 150 + 200} \right)}}\\
\therefore {x_{CM}} = 0.278
\end{array}$
Similarly, we need to calculate the y-coordinate also which can be calculated in the following.
$\begin{array}{l}
{y_{CM}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\
= \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0} \right) + \left( {200 \times 0.25\sqrt 3 } \right)}}{{\left( {100 + 150 + 200} \right)}}\\
\therefore {y_{CM}} = 0.192
\end{array}$
Hence, the coordinates of the centre of mass are given as $\left( {0.278,0.192} \right)$.
Note: We have derived the coordinates of the various masses by using simple rules of Pythagoras theorem. We take the first mass at origin and derive the coordinates of the rest of the particles based on given information and properties of the equilateral triangle.
Formula used:
The centre of mass of a system of mass can be given as
$C = \dfrac{{\sum {{m_i}r_i^2} }}{{\sum {{m_i}} }}$
Here ${m_i}$ represents the mass of the ith particle while ${r_i}$ represents the distance of the ith mass from the origin.
Detailed step by step solution:
The centre of mass of a system of masses is defined as the point on a body about which the whole mass of the given system is concentrated. Mathematically, it is equal to the ratio of sum of products of the masses and their distances from the origin to the sum of the given masses.
We are given three particles whose masses are given as
$\begin{array}{l}
{m_1} = 100g\\
{m_2} = 150g\\
{m_3} = 200g
\end{array}$
These three particles are arranged on the vertices of an equilateral triangle. Each side of the equilateral triangle has length of 0.5 m. We can draw the following diagram for this arrangement.
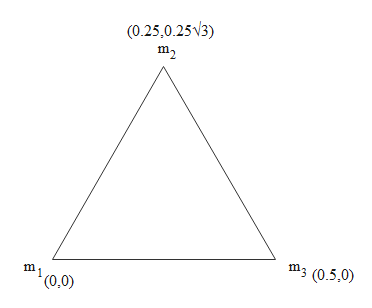
Now based on this diagram, we have three masses and their coordinates. Now we can find the coordinates of the centre of mass by using the formula given in equation (i). First, let us calculate the x-coordinate of the centre of mass. For this we will use the x-coordinates of the given masses. This is done in the following way.
$\begin{array}{l}
\left( {{x_1},{y_1}} \right) = \left( {0,0} \right)\\
\left( {{x_2},{y_2}} \right) = \left( {0.5,0} \right)\\
\left( {{x_3},{y_3}} \right) = \left( {0.25,0.25\sqrt 3 } \right)\\
{x_{CM}} = \dfrac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\
= \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0.5} \right) + \left( {200 \times 0.25} \right)}}{{\left( {100 + 150 + 200} \right)}}\\
\therefore {x_{CM}} = 0.278
\end{array}$
Similarly, we need to calculate the y-coordinate also which can be calculated in the following.
$\begin{array}{l}
{y_{CM}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3}}}{{{m_1} + {m_2}\, + {m_3}}}\\
= \dfrac{{\left( {100 \times 0} \right) + \left( {150 \times 0} \right) + \left( {200 \times 0.25\sqrt 3 } \right)}}{{\left( {100 + 150 + 200} \right)}}\\
\therefore {y_{CM}} = 0.192
\end{array}$
Hence, the coordinates of the centre of mass are given as $\left( {0.278,0.192} \right)$.
Note: We have derived the coordinates of the various masses by using simple rules of Pythagoras theorem. We take the first mass at origin and derive the coordinates of the rest of the particles based on given information and properties of the equilateral triangle.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Giving reasons state the signs positive or negative class 12 physics CBSE

Explain esterification reaction with the help of a class 12 chemistry CBSE

What is defined as a solenoid Depict a diagram with class 12 physics CBSE




