Question

Find the centre and radius of the circle ${{x}^{2}}+{{y}^{2}}+6x+8y-96=0$ .

Answer 1

Hint: We are provided by the equation of circle and are asked to find the centre and radius of the circle which can easily be found by comparing the given circle equation with general equations of a circle and then radius and centre of circle can be obtained.

Complete step-by-step answer:

Now, the circle is shape in a plane which consists of all that point whose distance is constant from a point lying inside it. The point from which all boundary points of a circle are equidistant is called the centre of a circle and the distance between centre and the outer boundary points is called radius of circle denoted by ‘ r ‘.
Now, there are two general equations of circle such as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where ( a, b ) represents the point of centre of a circle and r denotes the radius of circle.
Another form, is ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , where g ,f and c are constants
Now, to find the radius and centre of circle, we have two concepts which are, ( - g, - f ) represents the centre of circle and radius of circle that is r is equals to, $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
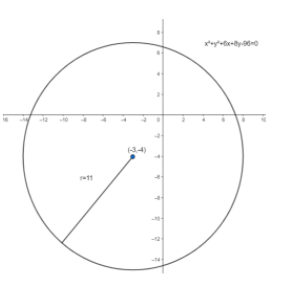
So, in question we are given that the equation of the circle is ${{x}^{2}}+{{y}^{2}}+6x+8y-96=0$ .
On comparing circle ${{x}^{2}}+{{y}^{2}}+6x+8y-96=0$ with the general equation of circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ , where g, f and c are constants we get
2g = 6 and 2f = 8 and c = -96
On simplifying we get,
g = 3 and f = 4 and c = -96
for, centre of circle we have ( - g, - f ),
putting value of g = 3 and f = 4, we get
centre of circle ${{x}^{2}}+{{y}^{2}}+6x+8y-96=0$ is equals to ( -3, -4 )
and for radius of circle we have $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
putting value of f , g and c in $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$, we get
$r=\sqrt{{{3}^{2}}+{{4}^{2}}-(-96)}$
On simplifying we get,
$r=\sqrt{9+16+96}$
Again on simplifying we get,
$r=\sqrt{121}$
On solving, we get
r = 11 cm
Hence, the centre and radius of circle ${{x}^{2}}+{{y}^{2}}+6x+8y-96=0$ are ( -3 , -4 ) and 1 cm.

Note: While solving numerical based on circles, one must know the both general equations of circles as it helps in solving the problem. The above question can also be solved by using the first general equation making the given circle equation into a form of general equation using completing the square method.