Question

Find the area of the triangle whose vertices are:
$(i) (2,3), ( - 1,0), (2, - 4)$
$(ii) ( -5, -1), (3, -5), (5,2)$

Answer 1

Hint: Basically, the area of triangle is defined as the total region that is enclosed by the three sides of any particular triangle.
To solve such types of questions we need to remember the formula for the area of the triangle.
Area of triangle =$\dfrac{1}{2}\left[ {{X_1}({Y_2} - {Y_3}) + {X_2}({Y_3} - {Y_1}) + {X_3}({Y_1} - {Y_2})} \right]$
By putting the values of vertices in the above formula, we will get the area of the triangle.

Complete step-by-step answer:
(i). As mentioned in the question, we have to find its area of the triangle whose coordinates of the vertices of the triangle $A$$(2,3),$ $B$$( - 1,0)$ & $C(2, - 4)$
               

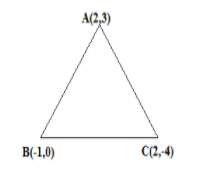
Area of triangle $ABC$
Formula for Area of triangle $ABC$=$\dfrac{1}{2}\left[ {{X_1}({Y_2} - {Y_3}) + {X_2}({Y_3} - {Y_1}) + {X_3}({Y_1} - {Y_2})} \right]$
Here,
${X_1} = 2,{Y_1} = 3$
${X_2} = - 1,{Y_2} = 0$
${X_3} = 2,{Y_3} = - 4$
Putting the values in the above formula
We can get the area of the triangle as
∴Area for the triangle $ABC$=$\dfrac{1}{2}\left[ {2(0 - ( - 4)) + ( - 1)( - 4 - 3) + 2(3 - 0)} \right]$
 On adding the brackets terms, we get
  =$\dfrac{1}{2}\left[ {2(4) + ( - 1)( - 7) + 2(3)} \right]$
Multiplying the terms we get,
 =$\dfrac{1}{2}\left[ {8 + 7 + 6} \right]$
On some simplification we get,
 =$\dfrac{1}{2}\left[ {21} \right]$
Dividing the terms, we get
=$10.5$ square unit
Hence we required the area of the triangle.

(ii). It is given that the vertices of triangle be $P( - 5, - 1),Q(3, - 5),R(5,2)$
               

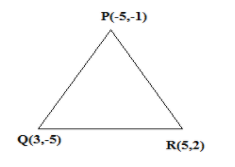
Area of triangle $PQR$
Area of the triangle $ = \dfrac{1}{2}\left[ {{X_1}({Y_2} - {Y_3}) + {X_2}({Y_3} - {Y_1}) + {X_3}({Y_1} - {Y_2})} \right]$
Here,
 ${X_1} = - 5,{Y_1} = - 1$
${X_2} = 3,{Y_2} = - 5$
${X_3} = 5,{Y_3} = 2$
Putting the values in the above formula
Area for the triangle PQR=$\dfrac{1}{2}\left[ {(( - 5)( - 5 - 2) + 3(2 - ( - 1) + 5( - 1 - ( - 5))} \right]$
On adding the brackets terms and negative sign, we get
$ = \dfrac{1}{2}\left[ { - 5( - 7) + 3(2 + 1) + 5( - 1 + 5)} \right]$
  $ = \dfrac{1}{2}\left[ { - 5( - 7) + 3(3) + 5(4)} \right]$
Multiplying the terms we get,
$ = \dfrac{1}{2}\left[ {35 + 9 + 20} \right]$
On some simplification we get,
$ = \dfrac{1}{2}\left[ {64} \right]$
Dividing the terms, we get
 $ = 32$ Sq. unit

Note: Here the possibility of mistake in the formula to find the area of triangle written as: if they do not know about the formula for calculation of the area of a triangle whose vertices are given
The formula that we can use to find the area of a triangle instead of with vertices as above mentioned. Area of triangle = $\dfrac{1}{2}\left[ {{x_1}({y_2} - {y_3}) + {x_2}({y_3} - {y_1}) + {x_3}({y_1} - {y_2})} \right]$
The coordinates of each vertex noted properly. One must also watch out for any calculation mistake while using the formula as well as simplification steps involved.