Question

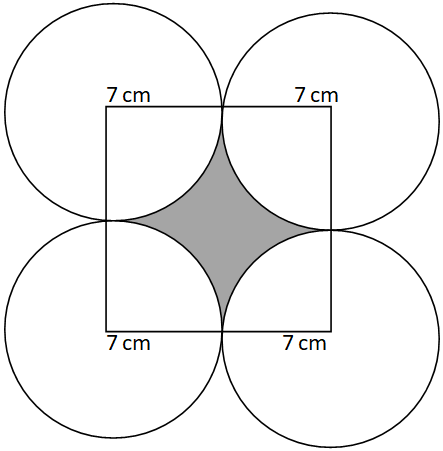
Find the area of the shaded region in the figure shown

Answer 1

Hint- In order to solve such a question, find the relationship between the area of a square, the area of four sectors of the circle and the area of the shaded region. Also establish some relationship between the area of four sectors.

Complete step-by-step answer:
Given that: radius of four circles $ = 7cm$
So the side of the square $ = 2 \times 7cm = 14cm$
Since these four circles have the same radius and are equal in area so they must be subtending at the right angle at the square.
From the figure we can see that
Area of the shaded region = Area of square – sum of area of four sectors subtending right angle.
Since, all the circles are equal and sectors are subtending at the right angle. So, area of all the four sectors are also equal and sum of the area of these 4 equal sector is equal to the area of circle of same radius i.e. $7cm$
Sum of area of four sectors
 \[
   = 4 \times \left( {\dfrac{1}{4} \times \pi {r^2}} \right) \\
   = \pi {r^2} \\
   = \pi {\left( 7 \right)^2} \\
   = \dfrac{{22}}{7} \times 7 \times 7 \\
   = 154c{m^2} \\
 \]
Area of the square
$
   = {\left( {{\text{side}}} \right)^2} \\
   = {\left( {14} \right)^2} \\
   = 14 \times 14 \\
   = 196c{m^2} \\
 $
So the area of the shaded portion
$
   = 196c{m^2} - 154c{m^2} \\
   = 42c{m^2} \\
 $
Hence, the area of the shaded portion is $42c{m^2}$ .

Note- In order to solve such questions related to area, figure plays a vital role in establishing the relationship between the area of the portion to be found out and the area of the given geometrical figures known. Formulas of area of sector and the area of squares must be remembered.