Question

 Find the area of the region enclosed between two circles: \[{{x}^{2}}+{{y}^{2}}=4\] and \[{{\left( x-2 \right)}^{2}}+{{y}^{2}}=4\].

Answer 1

Hint: Find center and radius of the given circles by comparing them to the standard equation of circle \[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\] where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is the center and ‘r’ is the radius. Now draw these circles on the coordinate axis and get the bounded region between them. Find the intersection point of the two circles. Area of any curve f(x) with the x-axis from x = a to x = b is given as \[\int\limits_{a}^{b}{f(x)dx}\]. Use this relation for further getting the area of the bounded region.

Complete step-by-step answer:
 Here we have two circles \[{{x}^{2}}+{{y}^{2}}=4\] and \[{{\left( x-2 \right)}^{2}}+{{y}^{2}}=4\] and hence, we need to determine the area enclosed within them.
So equations of circles are,
\[{{x}^{2}}+{{y}^{2}}=4.....(1)\]
\[{{\left( x-2 \right)}^{2}}+{{y}^{2}}=4.....(2)\]
We know that the standard equation of a circle is given as:
\[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}.....(3)\]
where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is center and ‘r’ is the radius of the circle.
It means that center and radius of both the circles are given as:
First circle from equation (1) as:
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}=4 \\
 & {{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( 2 \right)}^{2}} \\
\end{align}\]
Center = (0, 0)
Radius = 2
Second circle from equation (2) as:
\[{{\left( x-0 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( 2 \right)}^{2}}\]
Center = (2, 0)
Radius = 2
Now we can draw diagram of both the circles on coordinate axis as:

Now we can calculate the intersection points of both the circles as:
We have \[{{x}^{2}}+{{y}^{2}}=4\]
Put value of \[{{y}^{2}}\] from the first equation in second equation i.e. replace \[{{y}^{2}}\] by \[4-{{x}^{2}}\] equation. So we get:
\[\begin{align}
  & {{\left( x-2 \right)}^{2}}+4-{{x}^{2}}=4 \\
 & {{x}^{2}}+4-4x+4-{{x}^{2}}=4 \\
 & 4-4x=0 \\
 & 4(1-x)=0 \\
 & 1-x=0 \\
 & x=1 \\
\end{align}\]
Now we can put x = 1 to the equation \[{{x}^{2}}+{{y}^{2}}=4\], so we get:
\[\begin{align}
  & {{\left( 1 \right)}^{2}}+{{y}^{2}}=4 \\
 & {{y}^{2}}=4-1=3 \\
 & y=\pm \sqrt{3} \\
\end{align}\]
Hence points A and B can be given as \[\left( 1,\sqrt{3} \right)\] [first quadrant] and \[\left( 1,-\sqrt{3} \right)\] [fourth quadrant] respectively. It means line AB will be given as x = 1. Now we can draw diagram as:

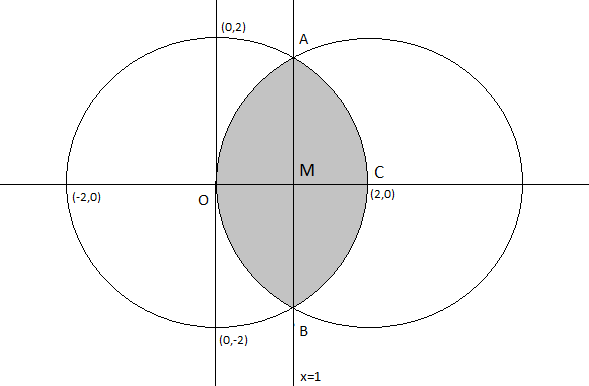
Now we can get area of the shaded region i.e. area of OACBO = area of region OACMO + area of OBCMO
Now by symmetry about the x-axis of both the circles, we get as follows that the area of OACMO and OBCMO will be equal. So we get:
Area of shaded region \[=2\times \] area of OACMO
We already know that area of any curve f(x) can be calculated with x-axis and from x = a to x = b as:
\[=\int\limits_{a}^{b}{f(x)dx}=\int\limits_{a}^{b}{ydy}.....(4)\]
Hence, the area of the region OAMO can be calculating by integrating the curve \[{{\left( x-2 \right)}^{2}}+{{y}^{2}}=4\] from x = 0 to x = 1 and similarly, area of region ACMA can be calculated by integrating the circle \[{{x}^{2}}+{{y}^{2}}=4\] from x = 1 to x = 2.
So we get:
Area of shaded region = 2 [area of OACMO] =2 [area of OAMO + area of ACMO]…..(5)
Now we can calculate value of y in terms of ‘x’ of first circle from equation (1) as:
\[\begin{align}
  & {{\left( x-2 \right)}^{2}}+{{y}^{2}}=4 \\
 & {{y}^{2}}=4-{{x}^{2}} \\
 & y=\sqrt{4-{{x}^{2}}}....(6) \\
\end{align}\]
Similarly, value of y for the second circle from the equation (2) as:
\[\begin{align}
  & {{\left( x-2 \right)}^{2}}+{{y}^{2}}=4 \\
 & {{y}^{2}}=4-{{\left( x-2 \right)}^{2}} \\
 & y=\sqrt{4-{{\left( x-2 \right)}^{2}}}.....(7) \\
\end{align}\]
Now we can get area of shaded region from the equation (5), (6) and (7) as:
Area of shaded region \[2\left[ \int\limits_{0}^{1}{\sqrt{4-{{\left( x-2 \right)}^{2}}}dx}+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx} \right]\]
Now we know the integration of \[\sqrt{{{a}^{2}}-{{x}^{2}}}\] can be given as:
\[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=}\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\left( \dfrac{x}{a} \right)+C.....(8)\]
Hence, area of the shaded region is given as:
\[\begin{align}
  & =2\left[ \left( \dfrac{x-2}{2}\sqrt{4-{{\left( x-2 \right)}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\dfrac{x-2}{2} \right)_{0}^{1}+\left( \dfrac{x}{2}\sqrt{4-{{x}^{2}}}+\dfrac{4}{2}{{\sin }^{-1}}\dfrac{x}{2} \right)_{1}^{2} \right] \\
 & =2\left[ \left( \dfrac{-1}{2}\sqrt{3}+2{{\sin }^{-1}}\left( \dfrac{-1}{2} \right) \right)-\left( -1\sqrt{4-4}+2{{\sin }^{-1}}(-1) \right)+\left( \dfrac{2}{2}\sqrt{4-4}+2{{\sin }^{-1}}(1)-\left( \dfrac{1}{2}\sqrt{3}+\dfrac{4}{2}{{\sin }^{-1}}\dfrac{1}{2} \right) \right) \right] \\
\end{align}\]
We know the values,
\[{{\sin }^{-1}}\dfrac{1}{2}=\dfrac{\pi }{6},{{\sin }^{-1}}\left( \dfrac{-1}{2} \right)=\dfrac{-\pi }{6},{{\sin }^{-1}}2=\dfrac{\pi }{2},{{\sin }^{-1}}(-1)=\dfrac{-\pi }{2}\]
So we get:
Area of the shaded region is given as:
\[\begin{align}
  & =2\left[ \dfrac{-\sqrt{3}}{2}+2\left( \dfrac{-\pi }{6} \right)+\dfrac{2\pi }{2}+\dfrac{2\pi }{2}-\dfrac{\sqrt{3}}{2}-\dfrac{2\pi }{6} \right] \\
 & =2\left[ \dfrac{-\sqrt{3}}{2}-\dfrac{\sqrt{3}}{2}-\dfrac{2\pi }{6}-\dfrac{2\pi }{6}+2\pi \right] \\
 & =2\left[ -\sqrt{3}-\dfrac{4\pi }{6}+2\pi \right]=-2\sqrt{3}+2\left( 2\pi -\dfrac{4\pi }{6} \right) \\
 & =\dfrac{8\pi }{3}-2\sqrt{3} \\
\end{align}\]
Hence area of the shaded region is \[\left( \dfrac{8\pi }{3}-2\sqrt{3} \right)uni{{t}^{2}}\].

Note: One may calculate the area of the shaded region by integrating the curve with respect to ‘y’ as well. Equation by this approach would be given as:
\[=2\left[ \int\limits_{0}^{\sqrt{3}}{\sqrt{4-{{y}^{2}}}-\int\limits_{0}^{\sqrt{3}}{\left( 2+\sqrt{4-{{y}^{2}}} \right)dy}} \right]\]
Don’t go wrong with the limits of the shaded region, i.e. one may put the limits of the integrals in the solution. So take care of it as well.
One may go wrong if he/ she calculates the bounded area combining the area of the shaded region in the first quadrant and fourth. One will get area as ‘0’ because areas will cancel out as the first quadrant will give positive area and the fourth quadrant will have negative (lying below x-axis). One can correct this approach by taking mod to the areas in the first and the fourth quadrant. Don’t confuse this approach as well and always try to observe some similarity with shaded region areas.