Find the area of the region bounded by the curve $y={{x}^{2}}$ and the line y = 4.
Answer
Verified360k+ views
Hint: The curve $y={{x}^{2}}$ is symmetrical to the y-axis and the line y = 4 restricts the region bounded by a parabola $y={{x}^{2}}$. So, we will first find the area of a region bounded by the y-axis, curve $y={{x}^{2}}$ in the first quadrant and the line y = 4, and then multiply it by 2 to get the required area.
Complete step-by-step answer:
It is given in the question that the region is bounded by the curve $y={{x}^{2}}$ and the line y = 4.
We have to find out the area bounded by the curve $y={{x}^{2}}$ and the line y = 4.
Let us assume that the line AB represents y = 4 in the diagram and curve AOB represent the curve $y={{x}^{2}}$ in the diagram.
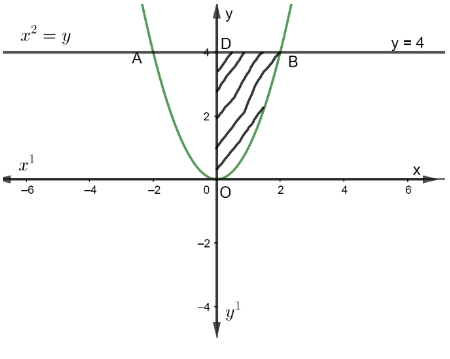
Now, from the figure, we can see that we have to find the area of the region AOBA.
From the diagram, we can say that AOB is a parabola which is symmetrical about the y-axis.
So, area of region AODA = area of region BODB.
Also, we have to find the area bounded by the region AOBA.
So, area of the region (AOBA) = 2 x Area(BODB).
Also, area of region (BODB),
$=\int_{0}^{4}{xdy}..........\left( 1 \right)$
We have given that in the question,
$\begin{align}
& {{x}^{2}}=y \\
& \Rightarrow x=\pm \sqrt{y} \\
\end{align}$
As we are finding the area BODB which is lying in the first quadrant. So, we will consider only $x=+\sqrt{y}$ and neglect $x=-\sqrt{y}$ because the first quadrant has positive abscissa and positive ordinate.
So, putting the value of $x=+\sqrt{y}$ in equation (1), we get,
$\begin{align}
& =\int_{0}^{4}{\sqrt{y}}dy \\
& =\int_{0}^{4}{{{\left( y \right)}^{\dfrac{1}{2}}}.}\ dy...........\left( 2 \right) \\
\end{align}$
We know that from basic integration,
$\int_{0}^{a}{{{\left( y \right)}^{n}}.\ dy=\left[ \dfrac{{{y}^{n+1}}}{n+1} \right]_{0}^{a}}$
Applying basic integration on equation (2), we get,
$\begin{align}
& =\left[ \dfrac{{{y}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right]_{0}^{4} \\
& =\left[ \dfrac{{{y}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{0}^{4} \\
\end{align}$
Now, putting the value of given limits, we get,
$\begin{align}
& =\left[ \dfrac{{{\left( 4 \right)}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]-\left[ \dfrac{{{0}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right] \\
& =\left[ \dfrac{{{\left( {{\left( 2 \right)}^{2}} \right)}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]=0 \\
& =\dfrac{{{\left( 2 \right)}^{3}}}{\dfrac{3}{2}} \\
& =\dfrac{8}{\dfrac{3}{2}} \\
& =\dfrac{8\times 2}{3} \\
& =\dfrac{16}{3} \\
\end{align}$
So, the area bounded by the region $BODB=\dfrac{16}{3}$.
Also, the area bounded by the region (AOBA) = 2 x (area of BODB)
Now, putting the value of the area of region BODB, we get,
$\begin{align}
& =2\times \dfrac{16}{3} \\
& =\dfrac{32}{3} \\
\end{align}$
Thus, the area bounded by the region $AOBA=\dfrac{32}{3}$.
Note: The alternative method of this question will be:
Step 1: We will find the area bounded by the region BODB.
Step 2: We will find the area bounded by the region AODA.
Step 3: Adding the area of AODA and area of BODA to get the required area AOBA.
Complete step-by-step answer:
It is given in the question that the region is bounded by the curve $y={{x}^{2}}$ and the line y = 4.
We have to find out the area bounded by the curve $y={{x}^{2}}$ and the line y = 4.
Let us assume that the line AB represents y = 4 in the diagram and curve AOB represent the curve $y={{x}^{2}}$ in the diagram.
Now, from the figure, we can see that we have to find the area of the region AOBA.
From the diagram, we can say that AOB is a parabola which is symmetrical about the y-axis.
So, area of region AODA = area of region BODB.
Also, we have to find the area bounded by the region AOBA.
So, area of the region (AOBA) = 2 x Area(BODB).
Also, area of region (BODB),
$=\int_{0}^{4}{xdy}..........\left( 1 \right)$
We have given that in the question,
$\begin{align}
& {{x}^{2}}=y \\
& \Rightarrow x=\pm \sqrt{y} \\
\end{align}$
As we are finding the area BODB which is lying in the first quadrant. So, we will consider only $x=+\sqrt{y}$ and neglect $x=-\sqrt{y}$ because the first quadrant has positive abscissa and positive ordinate.
So, putting the value of $x=+\sqrt{y}$ in equation (1), we get,
$\begin{align}
& =\int_{0}^{4}{\sqrt{y}}dy \\
& =\int_{0}^{4}{{{\left( y \right)}^{\dfrac{1}{2}}}.}\ dy...........\left( 2 \right) \\
\end{align}$
We know that from basic integration,
$\int_{0}^{a}{{{\left( y \right)}^{n}}.\ dy=\left[ \dfrac{{{y}^{n+1}}}{n+1} \right]_{0}^{a}}$
Applying basic integration on equation (2), we get,
$\begin{align}
& =\left[ \dfrac{{{y}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right]_{0}^{4} \\
& =\left[ \dfrac{{{y}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]_{0}^{4} \\
\end{align}$
Now, putting the value of given limits, we get,
$\begin{align}
& =\left[ \dfrac{{{\left( 4 \right)}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]-\left[ \dfrac{{{0}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right] \\
& =\left[ \dfrac{{{\left( {{\left( 2 \right)}^{2}} \right)}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]=0 \\
& =\dfrac{{{\left( 2 \right)}^{3}}}{\dfrac{3}{2}} \\
& =\dfrac{8}{\dfrac{3}{2}} \\
& =\dfrac{8\times 2}{3} \\
& =\dfrac{16}{3} \\
\end{align}$
So, the area bounded by the region $BODB=\dfrac{16}{3}$.
Also, the area bounded by the region (AOBA) = 2 x (area of BODB)
Now, putting the value of the area of region BODB, we get,
$\begin{align}
& =2\times \dfrac{16}{3} \\
& =\dfrac{32}{3} \\
\end{align}$
Thus, the area bounded by the region $AOBA=\dfrac{32}{3}$.
Note: The alternative method of this question will be:
Step 1: We will find the area bounded by the region BODB.
Step 2: We will find the area bounded by the region AODA.
Step 3: Adding the area of AODA and area of BODA to get the required area AOBA.
Last updated date: 26th Sep 2023
•
Total views: 360k
•
Views today: 9.60k
