Question

Find the area of the quadrilateral ABCD, in which AB = 7cm, BC = 6cm, CD = 12cm, DA = 15cm and AC = 9cm. The area is given as \[74.98c{{m}^{2}}\]. State whether the answer given is correct or not?
a.True
b.False

Answer 1

Hint: Draw the quadrilateral ABCD with the given sides and diagonal. Consider the 2 triangles formed and find their area using Heron’s formula, as you know all the sides.

Complete step-by-step answer:

Let us first draw a rough figure of quadrilateral ABCD. The 4 sides of the quadrilateral are AB, BC, CD and DA. Thus the length of these sides are AB = 7cm, BC = 6cm, CD = 12cm and DA = 15cm. AC is the diagonal of the quadrilateral ABCD, whose length is 9cm. Thus you can see the rough figure of quadrilateral ABCD.

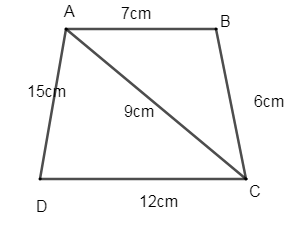
Let us consider the 2 triangles formed in the quadrilateral, \[\Delta ADC\] and \[\Delta ABC\].
Let us first find the area of \[\Delta ADC\].
We know that area of a triangle = \[\dfrac{1}{2}bh\], when we know the height. But for this particular figure, we can’t use this formula.
Hence we can use Heron’s formula, which gives the area of a triangle when the lengths of all three sides are known.
It is given as,
Area, \[A=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\], where a, b, c are the sides of the triangle and s is the perimeter, \[s=\dfrac{a+b+c}{2}\].
Here in \[\Delta ADC\], a = 15 cm, b =12 cm and c = 9cm.
Hence, \[s=\dfrac{15+12+9}{2}=\dfrac{36}{2}=18\]cm
Now let us substitute these values in Heron's formula.
\[A=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}\]
\[A=\sqrt{18\left( 18-15 \right)\left( 18-12 \right)\left( 18-9 \right)}\], let us simplify it
\[\begin{align}
  & A=\sqrt{18\times 3\times 6\times 9}=\sqrt{18\times 18\times 9}=\sqrt{{{18}^{2}}\times 9} \\
 & A=\sqrt{{{18}^{2}}\times {{3}^{2}}}=18\times 3=54c{{m}^{2}} \\
\end{align}\]
Hence, we got the area of \[\Delta ADC\] as \[54c{{m}^{2}}\].
\[\therefore ar\left( \Delta ADC \right)=54c{{m}^{2}}-(1)\]
Now let us find the area of \[\Delta ABC\], using heron’s formula.
In this triangle, a = 7cm, b = 6cm and c = 9cm.
\[\therefore s=\dfrac{a+b+c}{2}=\dfrac{7+6+9}{2}=\dfrac{22}{2}=11\], now let us substitute
\[\begin{align}
  & A=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}=\sqrt{11\left( 11-7 \right)\left( 11-6 \right)\left( 11-9 \right)} \\
 & A=\sqrt{11\times 4\times 5\times 2}=\sqrt{11\times 40}=\sqrt{440}=\sqrt{4\times 110}=2\sqrt{110} \\
\end{align}\]
Hence, we got the area of \[\Delta ABC\] as \[2\sqrt{110}c{{m}^{2}}\].
i.e. \[ar\left( \Delta ABC \right)=2\sqrt{110}-(2)\]
Hence area of quadrilateral ABCD = area of \[\Delta ADC\] + area of \[\Delta ABC\]
                                                             = ar (\[\Delta ADC\]) + ar (\[\Delta ABC\])
Now, substitute the value of equation (1) and (2).
Area of quadrilateral ABCD = \[54+2\sqrt{110}\]
                                                 \[\begin{align}
  & =54+2\times 10.49 \\
 & =54+20.98 \\
 & =74.98c{{m}^{2}} \\
\end{align}\]
Hence, we got the area of the quadrilateral as \[74.98c{{m}^{2}}\], which is same as the given answer. Hence the statement and given answer is correct.
\[\therefore \] Option (a) is correct.

Note: It is important that you draw a rough figure of the quadrilateral so that you get the idea of how to find the area. As you get 2 triangles, find them using Heron’s formula. You should remember this particular formula because the entire solution is based on it.