Question

Find the area of the quadrilateral ABCD. AC = 22cm, BM = 3cm, DN = 3cm and BM $\bot $ AC, DN $\bot $ AC.

Answer 1

Hint: Here, we need to first draw the diagram and then calculate the area of the quadrilateral by calculating the area of two triangles with a common base and add them together. The summation of the two areas of the triangles will give you the required result.

Complete step-by-step answer:
Let us first draw the diagram that has been given in the question with the given data.

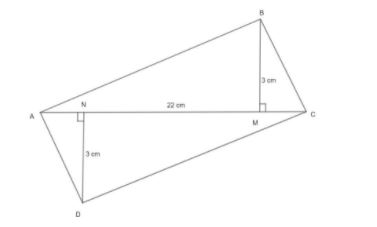
From the above diagram we can see that there are two triangles, triangle ABC and triangle ADC. They both have a common base and the height of the triangles are also equal which is 3 cm. The common base is 22 cm.
In the question, we have also been given that BM $\bot $ AC, DN $\bot $ AC.
Here, if we observe closely, we can see that the quadrilateral has been divided into two triangles by the diagonal AC. Now, we have two triangles, triangle ABC and triangle ADC.
Triangle ABC, has a height of 3 cm and a base of 22 cm and Triangle ADC has the same base and height values.
To find the area of the quadrilateral, we can just find the area of the triangle ABC and triangle ADC and add them together.
We know,
Area of triangle = $\dfrac{1}{2}$ (base)(height)
Therefore, area of triangle ABC = $\dfrac{1}{2}$(22)(3)
                                                         = (11)(3)
                                                         = 33
Now, we can also find the area of the triangle ADC with the similar values like triangle ABC, hence the area of the triangle ADC is 33 sq. cm.
Here, we know
Area of the quadrilateral ABCD = Area of the triangle ABC + Area of the triangle ADC
                                                        = 33 + 33
                                                        = 66
Hence, the area of the quadrilateral ABCD is 66 sq. cm.

Note: In this question, we did not use the perpendicular condition and go with the Pythagoras theorem, because we did not have some measurements which would have made the solution more tedious. But in the end, we would have got the same answer.