Question

Find the area of the minor segment of a circle of radius 42 cm, if length of the corresponding arc is 44 cm.

Answer 1

Hint: In this question, we will first find the value of angle $\theta $ which subtends on the arc of 44 cm; so that we can easily find the area of sector OADB by using this formula $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$. Then we will find the area of $\Delta OAB$. Now, we can easily find the area of the minor segment. Area of minor segment = Area of sector \[OADB\] – Area of $\Delta OAB$. In this way we can simply get our answer.

Complete step by step solution:
Figure based on the given information.

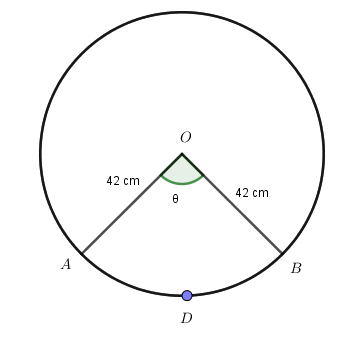
Step 1) First we will find angle of \[AOB\]
We know that;
Length of the arc of the minor segment = 44 cm
circle of radius = 42cm
Length of arc that subtends an angle $\theta $ = $\dfrac{\theta }{{360^\circ }} \times 2\pi r$
Where the value of \[\pi = \dfrac{{22}}{7}\], then
$ \Rightarrow 44\,$= $\dfrac{\theta }{{360^\circ }} \times 2 \times \dfrac{{22}}{7} \times 42$
On simplification, we get
$ \Rightarrow \,\,\,\theta = \dfrac{{44 \times 7 \times 360}}{{2 \times 22 \times 42}}$
$ \Rightarrow \,\,\,\theta = 60^\circ $
Step 2) Compute area of sector OADB
Area of sector $OADB = \dfrac{\theta }{{360^\circ }} \times \pi {r^2}$
\[ \Rightarrow \,\,\dfrac{{60^\circ }}{{360^\circ }} \times \dfrac{{22}}{7} \times 42 \times 42\]
 $ \Rightarrow \,\,924\,c{m^2}$
Thus Area of sector $OADB = 924\,c{m^2}$
Step 3) Compute the area of $\Delta OAB$
 OA = OB = radius
 So, angle $OAB = OBA$

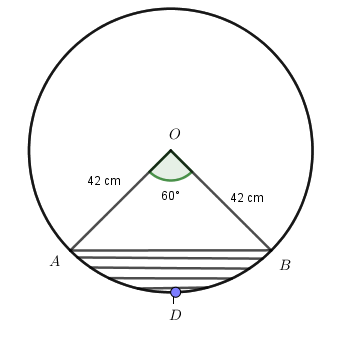
Let angle $OAB$and \[OBA\]be \[x\]
And angle $AOB = 60^\circ $
Sum of angles of a triangle OAB is $180^\circ $
$ \Rightarrow OAB + OBA + AOB = 180^\circ $
$ \Rightarrow x\, + \,x\, + \,60^\circ = 180^\circ $
$ \Rightarrow 2x = 180^\circ - 60^\circ $
$ \Rightarrow 2x = 120^\circ $
$\therefore \,\,x\,\, = \,\,60^\circ $
Thus, angle $OAB = OBA = 60^\circ $
Hence, we can now say that the triangle \[OAB\] is an equilateral triangle.
Area of $\Delta OAB = \dfrac{{\sqrt 3 }}{4} \times {a^2}$
$ \Rightarrow \,\,\dfrac{{\sqrt 3 }}{4} \times 42 \times 42$ (a = 42 cm, radius of a circle as well as side of a triangle)
$ \Rightarrow \,\,441\sqrt 3 \,c{m^2}$
Step 4) Now, we will compute the area of minor segment \[ADB\]
Area of a minor segment \[ADB\] = Area of a sector \[OADB\] – Area of $\Delta OAB$
\[ \Rightarrow \,\,924 - 441\sqrt 3 \]
$ \Rightarrow \,\,21(44 - 21\sqrt 3 )\,c{m^2}$
The area of minor segment is $21(44 - 21\sqrt 3 )\,c{m^2}$

Note: An important theorem we have used in this question;
If two sides of a triangle are equal, then the angles opposite to the same two sides are also equal.
In the above question, we have; OA = OB = radius it implies angle $OAB = OBA$.