Question

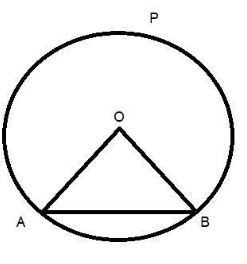
Find the area of the major segment APB in the given figure of a circle of radius
35cm and $\angle AOB = {90^0}$. Use $\left( {\pi = \dfrac{{22}}{7}} \right)$

Answer 1

Hint: To solve this question we have to understand the diagram and understand that the area of the major segment APB is equal to the area of the sector + area of the triangle.

Complete step-by-step answer:

We have to find area of major segment APB so it will be equal to:
Area of major sector AOPB + area of $\Delta AOB$
Here we have to add the area of the triangle because segment APB is formed by a combination of sector AOPB and triangle AOB.
We should understand from the figure that the area of the segment is nothing but the sum of area of sector and area of circle.
And we know
We know,
Area of sector = $\dfrac{\theta }{{2\pi }}\pi {r^2}$ and here $\theta = \dfrac{{3\pi }}{2}$ for sector AOPB
Area of triangle = $\dfrac{1}{2} \times {\text{multiplication of two consecutive sides}} \times {\text{sin of angle between them}}$
So, area = $\left( {\dfrac{{3\pi }}{2} \times \dfrac{1}{{2\pi }} \times \pi {r^2}} \right) + \dfrac{1}{2} \times r \times r \times \sin {90^0}$
 (Here side of triangle is equal to radius of circle as shown in diagram)
= $\dfrac{3}{4}\pi {r^2} + \dfrac{1}{2}{r^2}$
= $\dfrac{3}{4} \times \dfrac{{22}}{7} \times 35 \times 35 + \dfrac{1}{2} \times 35 \times 35$
$ = \dfrac{{5775}}{2} + \dfrac{{1225}}{2} = \dfrac{{5775 + 1225}}{2} = \dfrac{{7000}}{2} = 3500 cm^2$

Note: Whenever we get this type of question the key concept of solving is we are not able to find out the area of a big diagram then what we can do is break it into small areas and add all to get a bigger area. And we should also be familiar with many types of formulas for the area of triangles.