Question

Find the area of the greatest of isosceles triangles that can be inscribed in a given ellipse having its vertex coincide with one end of the major axis?

Answer 1

Hint: Consider the general equation of the ellipse. Draw the triangle inscribed in an ellipse, as the ellipse is symmetrical the 2 opposite vertices will have similar coordinates. Thus find the area of the triangle, differentiate the obtained equation, take \[z={{A}^{2}}\].

Complete step-by-step answer:
Let us consider the general equation of ellipse is,
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]

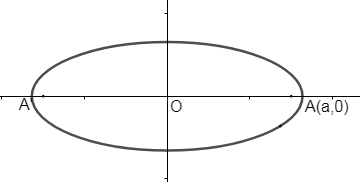
The major axis of the ellipse is AA’, which is along the x-axis. We know that the length of the major axis = 2a.
\[\therefore AA'=2a\].
Thus from the figure, we can say that OA’ = OA = a.
Hence we can form the coordinates of A as (a, 0).
An isosceles triangle inscribed in the ellipse it in the ellipse its vertex at one end of the major axis. Let \[\Delta PAP'\] be an isosceles triangle.
Thus the coordinates of P can be taken as (h, k) and coordinates of P’ (h, -k) as the ellipse is symmetric.
We need to find the greatest area of the triangle.
Let A be the area of the isosceles triangle \[\Delta PAP'\].
We know the area of the isosceles triangle \[\Delta PAP'\].
We know the area of the triangle = \[\dfrac{1}{2}\times \] base \[\times \] height.
\[A=\dfrac{1}{2}\times PP'\times AM\], (From the figure)

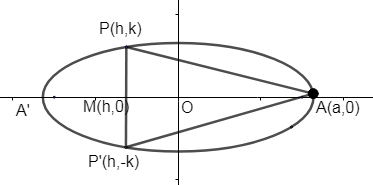
Let us consider a point M which lies on the x-axis. Thus the coordinates of M are (h, 0) as it lies on the x-axis.
Since point (h, k) lie on the ellipse.
\[\therefore \] (h, k) will satisfy the equation of ellipse.
Let us put x = h and y = k in the equation of ellipse.
\[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1\]
\[\therefore \dfrac{{{\left( h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( k \right)}^{2}}}{{{b}^{2}}}=1\]
By simplifying the expression,
\[\Rightarrow \dfrac{{{h}^{2}}{{b}^{2}}+{{k}^{2}}{{a}^{2}}}{{{a}^{2}}{{b}^{2}}}=1\]
Cross multiply the above,
\[\begin{align}
  & {{h}^{2}}{{b}^{2}}+{{k}^{2}}{{a}^{2}}={{a}^{2}}{{b}^{2}} \\
 & \therefore {{a}^{2}}{{k}^{2}}={{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}} \\
\end{align}\]
\[{{k}^{2}}=\dfrac{{{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}}}{{{a}^{2}}}\]
\[\therefore k=\sqrt{\dfrac{{{a}^{2}}{{b}^{2}}-{{b}^{2}}{{h}^{2}}}{{{a}^{2}}}}=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}-(1)\]
We know the values, P (h, k), P’ (h, -k), A (a, 0) and M (h, 0).
Now let us find PP’.
We can use the distance formula to find the distance which is given by
\[\begin{align}
  & \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \\
 & \therefore PP'=\sqrt{{{\left( h-h \right)}^{2}}+{{\left( -k-k \right)}^{2}}}=\sqrt{0+{{\left( -2k \right)}^{2}}}=\sqrt{4{{k}^{2}}} \\
 & \therefore PP'=2k \\
\end{align}\]
Similarly let us find AM using distance formula.
\[\begin{align}
  & AM=\sqrt{{{\left( a-h \right)}^{2}}+{{\left( 0-0 \right)}^{2}}} \\
 & AM=\sqrt{{{\left( a-h \right)}^{2}}} \\
 & AM=a-h \\
\end{align}\]
Thus we found the area of the triangle as, \[A=\dfrac{1}{2}\times PP'\times AM\].
\[\therefore A=\dfrac{1}{2}\times \left( a-h \right)\times 2k=\left( a-h \right)k\]
From equation (1), substitute the value of k to the above expression,
\[A=\dfrac{\left( a-h \right)}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}\]
Let us consider, \[z={{A}^{2}}\].
\[\begin{align}
  & \therefore z={{\left[ \left( \dfrac{a-h}{a} \right)\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}} \right]}^{2}} \\
 & z=\dfrac{{{\left( a-h \right)}^{2}}}{{{a}^{2}}}\left[ {{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}} \right] \\
\end{align}\]
\[z=\dfrac{{{\left( a-h \right)}^{2}}}{{{a}^{2}}}\times {{b}^{2}}\left[ {{a}^{2}}-{{h}^{2}} \right]\]
\[z={{\left( \dfrac{b}{a} \right)}^{2}}{{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right)\]
Now let us differentiate the above expression with respect to h.
\[\begin{align}
  & \dfrac{dz}{dh}=\dfrac{d}{dh}\left[ {{\left( \dfrac{b}{a} \right)}^{2}}{{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right) \right] \\
 & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\dfrac{d}{dh}\left[ {{\left( a-h \right)}^{2}}\left( {{a}^{2}}-{{h}^{2}} \right) \right] \\
\end{align}\]
Now let us use the product rule, as
\[uv=u'v+v'u\]
\[\begin{align}
  & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{d}{dh}{{\left( a-h \right)}^{2}}.\left( {{a}^{2}}-{{h}^{2}} \right)+\dfrac{d}{dh}\left( {{a}^{2}}-{{h}^{2}} \right).{{\left( a-h \right)}^{2}} \right] \\
 & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ 2\left( a-h \right)\left( -1 \right)\left( {{a}^{2}}-{{h}^{2}} \right)+\left( 0-2h \right){{\left( a-h \right)}^{2}} \right] \\
 & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2\left( a-h \right)\left( {{a}^{2}}-{{h}^{2}} \right)-2h{{\left( a-h \right)}^{2}} \right] \\
 & \dfrac{dz}{dh}={{\left( \dfrac{b}{a} \right)}^{2}}\left( -2 \right)\left( a-h \right)\left[ {{a}^{2}}-{{h}^{2}}+ha-{{h}^{2}} \right] \\
 & \dfrac{dz}{dh}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left( a-h \right)\left[ {{a}^{2}}+ha-2{{h}^{2}} \right] \\
\end{align}\]
Let us put, \[\dfrac{dz}{dh}=0\].
\[\begin{align}
  & -2{{\left( \dfrac{b}{a} \right)}^{2}}\left( a-h \right)\left[ {{a}^{2}}+ha-2{{h}^{2}} \right]=0 \\
 & \therefore \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)=0 \\
\end{align}\]
From the above expression, we know that
\[a-h=0\] and \[{{a}^{2}}+ah-2{{h}^{2}}=0\]
Thus by solving, \[a-h=0\], we get, a = h.
\[{{a}^{2}}+ah-2{{h}^{2}}=0\], add and subtract ah in this expression.
\[\begin{align}
  & {{a}^{2}}+ah-2{{h}^{2}}+ah-ah=0 \\
 & {{a}^{2}}+2ah-2{{h}^{2}}-ah=0 \\
 & {{a}^{2}}+2ah-ah-2{{h}^{2}}=0 \\
 & a\left( a+2h \right)-h\left( a+2h \right)=0 \\
 & \left( a-h \right)\left( a+2h \right)=0 \\
\end{align}\]
\[\therefore a-h=0\] and \[a+2h=0\].
\[\therefore h=a\] and \[h=\dfrac{-a}{2}\].
Thus we get h = a and \[h=\dfrac{-a}{2}\].
If h = a,
\[\therefore k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}\]
\[k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}}=0\], but this is not possible.
So, let us find \[\dfrac{{{d}^{2}}z}{d{{h}^{2}}}\], w.r.t ‘h’.
\[\begin{align}
  & \dfrac{dz}{dh}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right) \right] \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\dfrac{d}{dh}\left[ \left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right) \right] \\
\end{align}\]
Use the product rule to solve, \[uv=u'v+v'u\].
\[\begin{align}
  & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{d}{dh}\left( a-h \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)+\dfrac{d}{dh}\left( {{a}^{2}}+ah-2{{h}^{2}} \right)\left( a-h \right) \right] \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \left( -1 \right)\left( {{a}^{2}}+ah-2{{h}^{2}} \right)+\left( a-4h \right)\left( a-h \right) \right] \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -{{a}^{2}}-ah+2{{h}^{2}}+{{a}^{2}}-ah-4ah+4{{h}^{2}} \right] \\
\end{align}\]
Open the brackets and simplify the expression,
\[\dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2ah-4ah+6{{h}^{2}} \right]\]
Now let us put, \[h=\dfrac{-a}{2}\].
\[\begin{align}
  & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ -2a\left( \dfrac{-a}{2} \right)-4a\left( \dfrac{-a}{2} \right)+6{{\left( \dfrac{-a}{2} \right)}^{2}} \right] \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ {{a}^{2}}+2{{a}^{2}}+\dfrac{3}{2}{{a}^{2}} \right] \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left[ \dfrac{9{{a}^{2}}}{2} \right]=-2{{\left( \dfrac{b}{a} \right)}^{2}}\left( \dfrac{9{{a}^{2}}}{2} \right) \\
 & \dfrac{{{d}^{2}}z}{d{{h}^{2}}}=-9{{b}^{2}}<0 \\
\end{align}\]
\[\dfrac{{{d}^{2}}z}{d{{h}^{2}}}<0\] at \[h=\dfrac{-a}{2}\].
Therefore z is maximum when, \[h=\dfrac{-a}{2}\].
Thus the area will be maximum when, \[h=\dfrac{-a}{2}\].
Let us put \[h=\dfrac{-a}{2}\], in equation (1).
\[\begin{align}
  & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{\left( bh \right)}^{2}}} \\
 & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-{{b}^{2}}{{\left( \dfrac{-a}{2} \right)}^{2}}} \\
 & k=\dfrac{1}{a}\sqrt{{{\left( ab \right)}^{2}}-\dfrac{{{a}^{2}}{{b}^{2}}}{4}}=\dfrac{ab}{a}\sqrt{1-\dfrac{1}{4}} \\
 & k=b\sqrt{\dfrac{4-1}{4}}=\dfrac{b\sqrt{3}}{2} \\
\end{align}\]
Hence, we have \[h=\dfrac{-a}{2}\] and \[k=\dfrac{b\sqrt{3}}{2}\].
We need to find the maximum value of Area.
\[\begin{align}
  & A=\dfrac{1}{2}\times \left( a-h \right)\left( 2k \right) \\
 & A=\dfrac{1}{2}\left( a-\left( \dfrac{-a}{2} \right) \right)\times 2\left( \dfrac{b\sqrt{3}}{2} \right) \\
 & A=\dfrac{1}{2}\left( a+\dfrac{a}{2} \right)b\sqrt{3} \\
 & A=\dfrac{1}{2}\left( \dfrac{3a}{2} \right)b\sqrt{3} \\
 & A=\dfrac{3\sqrt{3}ab}{4} \\
\end{align}\]
Hence, we got the maximum area \[=\dfrac{3\sqrt{3}ab}{4}\].

Note: We did differentiation two times in \[\dfrac{dz}{dh}\], we got the value of k as zero. If k was not zero than \[\dfrac{{{d}^{2}}z}{d{{h}^{2}}}\] is not required to get the value of k. thus find the coordinates (h, k) and find the area. Here \[\dfrac{{{d}^{2}}z}{d{{h}^{2}}}\] should be less than zero.