Question

Find the area of quadrilateral whose one diagonal is \[25cm\]long and the lengths of perpendiculars from the other two vertices are \[16.4cm\]and \[11.6{\text{ }}cm\]respectively.

Answer 1

Hint: We will draw a diagram according to the given information in the question. Thereafter, we will calculate the area of the triangle separately, by using diagonal as a base of both the triangles and height will be $16.4$cm and $11.6$cm. Further, we will add the area of both the triangles to get the area of quadrilateral.
Area of triangle \[ = \dfrac{1}{2} \times base \times height\]


Complete step by step solution:

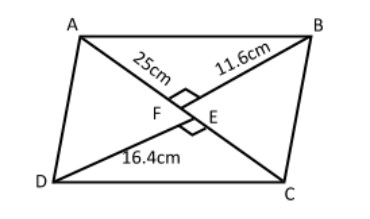
For calculating the area of quadrilateral $ABCD$
We will solve separately in two parts $\Delta ABC\,\,and\,\,\Delta ADC$
In $\Delta ADC$
$
  AC = 25cm \\
  DE = 16.4cm \\
 $
By using the formula of area
So area \[\Delta ADC = \dfrac{1}{2} \times base \times height\]
Here, base $ = 25cm$
And height$ = 16.4$, now but these value in the formula
Area $(\Delta ADC) = \dfrac{1}{2} \times 25 \times 16.4$
$ = 25 \times 8.2$
Area $(\Delta ADC) = 205.00c{m^2}$
Now, in $\Delta ABC$,
Area $(\Delta ABC) = \dfrac{1}{2} \times base \times height$
$AC(base) = 25cm$
$BF(height) = 11.6cm$
Now, put these values in the formula.
Area \[(\Delta ABC) = \dfrac{1}{2} \times 25 \times 11.6\]
$ = 25 \times 5.8$
$ = 145c{m^2}$
Now, we will add the area $(\Delta ABC)$ and area $(\Delta ADC)$to get the area of quadrilateral $ABCD$
Area quadrilateral of $ABCD = area(\Delta ABC) + area(\Delta ADC)$
$ = 145c{m^2} + 205c{m^2}$
$ = 350c{m^2}$
Therefore, the area of quadrilateral $ABCD$ is $350c{m^2}$


Note: Students must know the area of the triangle \[ = \dfrac{1}{2} \times base \times height\]. Students will find the area of two triangles then at these two areas to find the area of the quadrilateral.