Question

Find the area of a right-angled triangle, the radius of whose circumcircle measures \[8{\text{cm}}\], and the altitude drawn to the hypotenuses measures \[{\text{6cm}}\].

Answer 1

Hint: Here, we will use the formula for finding the area of a right-angled triangle as shown below:
\[{\text{Area of }}\Delta {\text{ABC = }}\dfrac{1}{2} \times b{\text{ase}} \times {\text{height}}\]

Complete step by step answer:
Step (1): First of all, we will draw the diagram according to the given information in the question where \[\Delta {\text{ABC}}\] is a right-angled triangle with a circumcircle having Centre O:

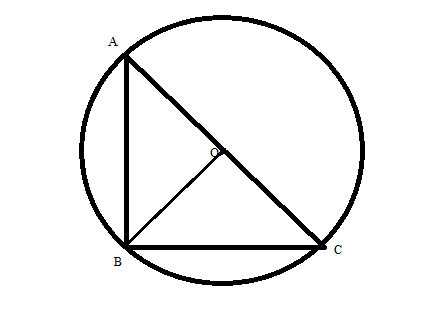
Where, \[{\text{AO}} = {\text{BO}} = {\text{CO}} = r = 8{\text{cm}}\].
Step 2: Now we will draw a perpendicular from the point \[{\text{B}}\]to the hypotenuse \[{\text{AC}}\] which touches it at the point \[{\text{D}}\] as shown below:

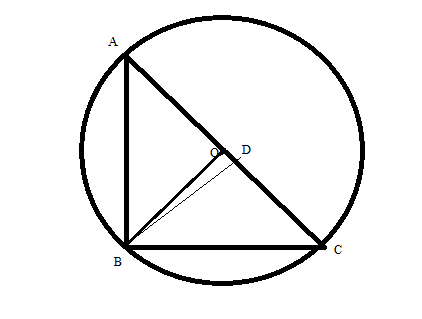
So, \[{\text{BD = 6cm}}\] (\[\because \] as given)
Step 3: As we know that the radius of the circle is equal so, \[{\text{AO}} = {\text{CO}}\] and for the hypotenuse of the triangle is equals to the sum of both the radius as shown below:
\[ \Rightarrow {\text{AO + CO = AC}}\]
By substituting the values of the radius \[{\text{AO}} = {\text{CO}} = r = 8{\text{cm}}\] in \[{\text{AO + CO = AC}}\], we get:
\[ \Rightarrow {\text{AC = 16cm}}\]
Step 4: Now, in the right-angled triangle \[\Delta {\text{ABC}}\], the altitude of the triangle is \[{\text{BD = 6cm}}\] and the hypotenuse is \[{\text{AC = 16cm}}\]. By using the formula of area of the triangle which states that area of right-angle triangle = \[\dfrac{1}{2} \times {\text{base}} \times {\text{height}}\], we get:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ABC = }}\dfrac{1}{2} \times 16 \times 6\] ……………. (1)
By solving the RHS side of the above expression (1), we get:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ABC = 48c}}{{\text{m}}^2}\]

The area of the triangle is \[{\text{48c}}{{\text{m}}^2}\].

Note:
Students needs to remember that the height circumcenter of a right-angle triangle is the midpoint of its hypotenuse:
\[ \Rightarrow {\text{Hypotenuse}} = 2 \times {\text{Radius of the circumcircle}}\]
In these questions, for finding the area of the triangle, we need to consider hypotenuse as a base and the altitude to the hypotenuse as height.