Question

How do you find the area of a Parallelogram without the height?

Answer 1

Hint: Here, we will use the Trigonometric Ratio of sine to find the height of the triangle, and by using the area of the triangle we will find the area of the congruent triangle in a Parallelogram. By using the area of the congruent triangles, we will find the area of the Parallelogram.

Formula Used:
We will use the following formula:
1. Area of a triangle is given by the formula \[ = \dfrac{1}{2}b \times h\] sq. units
2. Trigonometric Ratio: \[\sin \theta = \dfrac{{{\rm{Opp}}}}{{{\rm{Hyp}}}}\]

Complete Step by Step Solution:
We will find the area of the Parallelogram without the height.

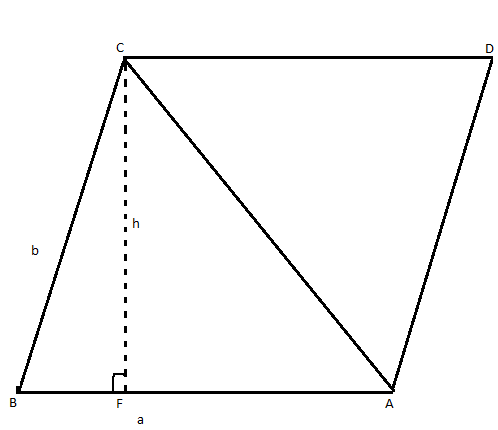
Let ABCD be a Parallelogram. Let \[AB = a;BC = b;\] be the sides of the Parallelogram and\[h\] be the height of the Parallelogram.
We are given that the height is unknown. Now, we will find the height of the Parallelogram by using the Area of the Triangle.
Now, we will find the height of the parallelogram by using the area of the triangles.
Trigonometric Ratio: \[\sin \theta = \dfrac{{Opp}}{{Hyp}}\]
Now, by using trigonometric ratio in the right angle triangle, we get
\[\sin B = \dfrac{{CF}}{{BC}}\]
By substituting the known values, we get
\[ \Rightarrow \sin B = \dfrac{h}{b}\]
Multiplying \[b\] on both sides, we get
\[ \Rightarrow h = b\sin B\]
Substituting the height and base in the area of the triangle, we get
Area of the Triangle \[ = \dfrac{1}{2} \times a \times b\sin B\]sq. units
We know that the diagonal of a Parallelogram divides the Parallelogram into two congruent triangles. Thus, the Area of the Parallelogram is twice the area of the triangle. Thus, we get
\[ \Rightarrow \] Area of the Parallelogram \[ = 2 \times \] Area of the Triangle sq. units
Now, by substituting the area of the triangle, we get
\[ \Rightarrow \] Area of the Parallelogram \[ = 2 \times \dfrac{1}{2} \times a \times b\sin B\] sq. units
Multiplying the terms, we get
\[ \Rightarrow \] Area of the Parallelogram \[ = a \times b\sin B\] sq. units

Therefore, the area of the Parallelogram is \[ab\sin B\] sq. units when the height is unknown.

Note:
We know that the Area of a Parallelogram is the region occupied by a Parallelogram in a two- dimensional Plane. We can also find the area of the Parallelogram by using the area of the Parallelogram even though height is not unknown.
We know that Area of a Parallelogram \[ = bh\] sq. units
Substituting the height and base in the area of the triangle, we get
\[ \Rightarrow \] Area of a Parallelogram \[ = ab\sin B\] sq. units
Therefore, the area of the Parallelogram is \[ab\sin B\] sq. units when the height is unknown.