Question

How do you find the area of a four sided polygon ?

Answer 1

Hint:Area of any figure explains the space taken by the enclosed figure when subjected to any surface, for different figures we have defined the formulae of calculating the area. In case of quadrilateral it explains any closed figure enclosed by four sides and having four vertices, and according to different properties followed by the shape, names are defined accordingly. A quadrilateral is a polygon with four sides.

Formulae Used:
\[\text{area of triangle} = \dfrac{1}{2} \times\text{base} \times\text{height}\]

Complete step by step answer:
 The given question asks to find the area of any polygon having four sides, to solve this we have to draw a polygon to explain the answer. Four sided polygon:

For this shape we can see that it can be equally divided into two right triangles,after dividing and naming the sides we get:

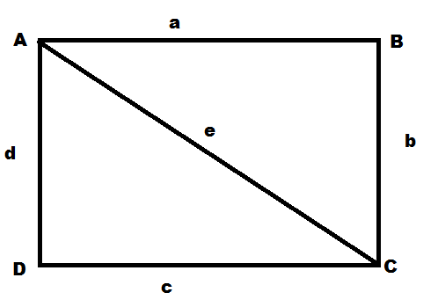
Here we get two triangle say triangle ABC and triangle ACD
Now we know that area of triangle is:
\[ \Rightarrow\text{area of triangle} = \dfrac{1}{2} \times\text{ base} \times \text{height}\]
Now for calculation of area of polygon we have to add the area of both the triangles, on solving we get:
For triangle $ABC$, base = $b$ and height = $a$.For triangle $ACD$, base = $d$ and height = $c$.
\[\text{area of polygon} = \text{ area of}\,\Delta ABC + \text{area of}\,\Delta ACD = \dfrac{1}{2} \times b \times a + \dfrac{1}{2} \times d \times c \\
\Rightarrow \text{area of polygon} = \dfrac{1}{2}ab + \dfrac{1}{2}dc \\
\Rightarrow \text{area of polygon}= \dfrac{1}{2}ab + \dfrac{1}{2}ab………(\text{since a = c and b = d}) \\
\Rightarrow \text{area of polygon} = \left( {\dfrac{1}{2} + \dfrac{1}{2}} \right)a \times b \\
\Rightarrow\text{area of polygon}= 1 \times a \times b \\
\therefore\text{area of polygon}= ab \\ \]
Hence, the area of a four sided polygon is $ab$.

Note: For finding the area of a regular polygon with the given sides, then either it’s a standard shape and the formulae of area is known to us, or if not given then just break the figure into two or different shapes whose formula is known and can solve accordingly, or by integration we have to solve the question.