Question

Find the area (in square units) of the region described by $A = \left\{ {\left( {x,y} \right)|y \geqslant {x^2} - 5x + 4,x + y \geqslant 1,y \leqslant 0} \right\}$.
(A) $\dfrac{{17}}{6}$
(B) $\dfrac{{13}}{6}$
(C) $\dfrac{{19}}{6}$
(D) $\dfrac{7}{2}$

Answer 1

Hint:Mark the points on the coordinate plane for better understanding and visualising the area bounded by the curves. Plot each of the curves with the regions of the area according to the inequality. This will give the bounded area. Use the concept that taking the definite integral of a curve will give you the area below that curve in that interval.

Complete step-by-step answer:

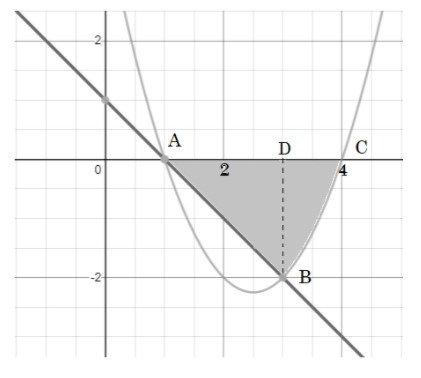
Let’s first try to understand the question using the coordinate plane. There are three inequalities given in the region A. First one, the curve$y \geqslant {x^2} - 5x + 4$, represents an upward parabola, the second one is $x + y \geqslant 1$, represents a straight line and then $y \leqslant 0$, which is the equation of x-axis.

Now, we should figure out the region that these curves enclose.
For $x + y \geqslant 1$, the inequality simply means that the region with all the points that satisfy the given inequality. For each $x = 0,y = 0$, we get an intercept as $1$.
Since the line does not pass through the origin, we put $\left( {x,y} \right) = \left( {0,0} \right)$ to check the region.
$ \Rightarrow $ For$\left( {x,y} \right) = \left( {0,0} \right)$, $x + y = 0 + 0 = 0$ which do not satisfy the inequality. Therefore, the region required will be on the opposite side of the origin.

For $y \geqslant {x^2} - 5x + 4$, the inequality simply means that the region with all the points that satisfy the given inequality. It is a curve representing the quadratic equation.$y \geqslant {x^2} - 5x + 4 \Rightarrow y \geqslant \left( {x - 4} \right)\left( {x - 1} \right)$, so it meets the x-axis on at $x = 4,1$.
Since the line does not pass through the origin, we put $\left( {x,y} \right) = \left( {0,0} \right)$ to check the region.
$ \Rightarrow $ For $\left( {x,y} \right) = \left( {0,0} \right)$, $0 \geqslant 0 - 0 + 4 \Rightarrow 0 \geqslant 4$ which did not satisfy the inequality. Therefore, the region required will be on the opposite side of the origin.

So, we get a region ABC in the third quadrant as shown in the above diagram.
Let’s check for the intersection points of line and parabola which are A and B.
For that we need to solve, $y = {x^2} - 5x + 4$ and $x + y = 1$. We can combine both of them as:
$ \Rightarrow 1 - x = {x^2} - 5x + 4$
It can be further solved to determine the value of $x$:
$ \Rightarrow {x^2} - 4x + 3 = 0$
$ \Rightarrow \left( {x - 1} \right)\left( {x - 3} \right) = 0$
Therefore, we get $x = 1,3$ $ \Rightarrow y = 1 - 1 = 0$ and $y = 1 - 3 = - 2$
So, hence we have common points as: $A\left( {1,0} \right)$ and $B\left( {3, - 2} \right)$
Therefore, we get the points as:$A\left( {1,0} \right)$,$B\left( {3, - 2} \right)$,$C\left( {4,0} \right)$ and $D\left( {3,0} \right)$
Area ABC $ = $ Area of triangle $\Delta ADB$+Area under parabola BC
And for the area we can take the integral of the parabola for $x \in \left( {3,4} \right)$
So, Area ABC $ = \dfrac{1}{2} \times AD \times DB + \int\limits_3^4 {\left( {{x^2} - 5x + 4} \right)} dx = \dfrac{1}{2} \times 2 \times 2 +
$ = 2 +
$ = 2 + \left( {\dfrac{{64 - 27}}{3} - \dfrac{5}{2} \times 7 + 4} \right) = 2 + \dfrac{{37}}{3} - \dfrac{{35}}{2} + 4 = \dfrac{{19}}{6}$
So, we calculated the required area as $\dfrac{{19}}{6}$

So, the correct answer is “Option C”.

Note:Try to draw a diagram and mark all the points on a coordinate plane. This will help you visualize better. An alternative approach for this question can be taken by integrating the equation of the line for $x \in \left( {1,3} \right)$ and then add the area under parabola for $x \in \left( {3,4} \right)$.Students should remember the integration formula of polynomial function i.e in general $\int {x^n} dx = \dfrac{x^{n+1}}{n}$ for solving these types of problems.