Question

How do you find the angle of the resultant vector?

Answer 1

Hint: Let us first know about vectors. Vectors are useful in physics because they can represent location, displacement, velocity, and acceleration visually. When drawing vectors, you often don't have enough room to draw them to the scale they represent, therefore it's crucial to specify what scale you're working with.

Complete step by step solution:
Let P and Q be two vectors acting at the same time at a location, represented in magnitude and direction by two adjacent sides OA and OD of a parallelogram OABD, as shown in figure.
Let R be the resultant vector and be the angle between P and Q. The consequent of P and Q is therefore represented by diagonal OB, according to the parallelogram law of vector addition.

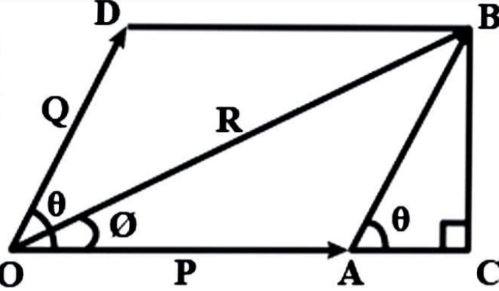
So,
$R = P + Q$
Expand A to C and draw BC perpendicular to OC at this point.
From triangle OCB
$O{B^2} = {C^2} + B{C^2}$
$ \Rightarrow $ $O{B^2} = {(OA + AC)^2} + B{C^2}$ ….$(1)$
In triangle ABC
$\cos \theta = \dfrac{{AC}}{{AB}}$
$ \Rightarrow $$AC = AB\,\cos \theta $
$ \Rightarrow $$AC = OD\,\cos \theta $
$AC = Q\cos \theta \,\,\,\,\,\,\,\,[AB = OD = Q]$
Also,
$\cos \theta = \dfrac{{BC}}{{AB}}$
$ \Rightarrow $\[\;BC{\text{ }} = {\text{ }}AB{\text{ }}sin\theta \]
$ \Rightarrow $\[BC{\text{ }} = {\text{ }}OD{\text{ }}sin\theta \]
$BC = Q{\text{ }}sin\theta \;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}\;{\text{ }}[{\text{ }}AB{\text{ }} = {\text{ }}OD{\text{ }} = {\text{ }}Q\;]$
Magnitude of resultant we will be:
Substituting value of AC and BC in $(1)$ we get
\[{R^2} = {(P + Qcos\theta )^2} + {(Qsin\theta )^2}\]
$ \Rightarrow $\[{R^2} = {P^2} + 2PQcos\theta + {Q^2}co{s^2}\theta + {Q^2}si{n^2}\theta \]
$ \Rightarrow $\[{R^2} = {P^2} + 2PQcos\theta + {Q^2}\]
$ \Rightarrow $\[R{\text{ }} = \;\sqrt {{P^2} + 2PQcos\theta + {Q^2}} \]
Now let us see the direction of Resultant:
Let $\phi $ be the angle made by the resultant R with P.
From triangle OBC,
\[tan\phi = \dfrac{{BC}}{{OC}} = \dfrac{{BC}}{{OA + AC}}\]
$ \Rightarrow $\[\;tan\phi = \dfrac{{Q\,\sin \theta }}{{P + Q\cos \theta }}\]
\[\phi = {\tan ^{ - 1}}\left( {\dfrac{{Q\sin \theta }}{{P + Q\cos \theta }}} \right)\]
This is the angle of the resultant vector.

Note:
We use vector values like displacement, acceleration, and force to launch satellites into the sky, target foes on the battlefield, do sophisticated calculations within computers, and even identify our location using GPS or a map. As a result, vectors play a crucial part in our lives.