Question

Find the angle of elevation of the sun, when the length of the shadow of a person is equal to $\sqrt 3 $ times his height.

Answer 1

Hint:-Here we have to go through by first making the diagram by the statement of the question and then by applying the rule of trigonometric ratio we will find our answer.

Complete step-by-step solution -
Here in the question it is given that the length of the shadow of a person is equal to $\sqrt 3 $ times his height.
Now let the height of the man be x.
Then according to the question the length of the shadow become $\sqrt 3 x$

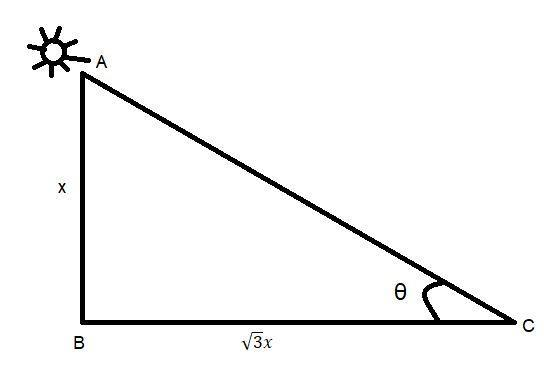
Now according to the figure we made we can say,
AB is the height of man and BC is the length of shadow and the angle of elevation is $\angle ACB = \theta $.
Now by applying the properties of trigonometric ratio we get,
$\tan \theta = \dfrac{{AB}}{{BC}} = \dfrac{x}{{\sqrt 3 x}} = \dfrac{1}{{\sqrt 3 }}$ As we know that by the property of trigonometric ratio, tan is the ratio of perpendicular to base i.e. $\tan \theta = \dfrac{p}{b}$.
And we know that the value of some trigonometric angles i.e. as we know $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$.
By comparing with $\tan \theta $ we get,
$\tan {30^0} = \dfrac{1}{{\sqrt 3 }} = \tan \theta $
By this we can clearly say that the value of $\theta = {30^0}$.
Hence the angle of elevation of the sun $\angle ACB = \theta = {30^0}$.

Note:-Whenever we face such a type of question the key concept for solving the question is to first sketch the diagram and denote the data that is given in the question. And we also know that the term angle of elevation denotes the angle from the horizontal upward to an object. An observer's line of sight would be above the horizontal. The term angle of depression denotes the angle from the horizontal downward to an object. And then by applying a trigonometric ratio we will get our answer.