Question

How do you find the angle of elevation of the sun if at 10 am on April 26, 2000, a building 300 feet high casts a shadow 50 feet long?

Answer 1

Hint: In this question, we are given the height of the building and the height of its shadow; we have to find the angle of elevation of the sun, that is, the angle between the shadow and the line joining the top of the building with the top of the shadow. Buildings are always perpendicular to the triangle, so the figure obtained is a right-angled triangle. We know that, trigonometric function tells us the relation between the sides of a right triangle and its angles, so we use the appropriate trigonometric function to find out the angle of elevation.

Complete step-by-step answer:

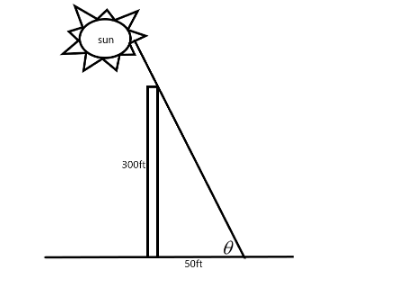
We know that –
 $ \tan \theta = \dfrac{{perpendicular}}{{base}} $
In this question, perpendicular is equal to the height of the building, that is, 300 feet and the base is equal to the height of the shadow, that is, 50 feet.
So,
 $
  \tan \theta = \dfrac{{300}}{{50}} \\
   \Rightarrow \tan \theta = 6 \\
   \Rightarrow \theta = {\tan ^{ - 1}}6 \\
   \Rightarrow \theta = 80.5^\circ \;
  $
Hence, the angle of elevation of the sun is $ 80.5^\circ $ .
So, the correct answer is “ $ 80.5^\circ $ ”.

Note: Trigonometric ratios are the ratios of two sides of a right-angled triangle; the sine function is the ratio of the perpendicular and the hypotenuse, cosine function is the ratio of the base and the hypotenuse and the tangent function is the ratio of the perpendicular and the hypotenuse. In this question, we know the measure of the perpendicular and the hypotenuse so we use the tangent function. To get the value of the angle, we use the knowledge of inverse trigonometric functions.