Question

Find the angle of elevation if an object is at a height of 50m on the tower and the distance between the observer and the foot of the tower is 50m.

Answer 1

Hint: Draw the diagram as the instructions given in the question, then use trigonometric law or identity for $\tan \theta $. After that solve it and find $\theta $.

Complete step-by-step answer:

In the question, we have to find the angle of elevation if an object is at height of 50m on the tower and the distance between the observer and the foot of the tower is 50m.

So, let’s represent the tower as AB and the object be situated at point A. Hence, we can represent it as in the diagram shown below.

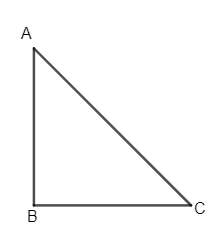
Here, we have to find the angle ACB, let’s represent it as $\theta $ .

So, $\angle ACB=\theta $

In the question, we are told that the object is at a height of 50m of the tower. So, we can say that the length of AB is 50m.

We also know that observer at point C is at a distance of 50m from the foot of the tower.

So, $AB=BC=50m$

Now, we will apply identity of trigonometric ratio, which is

$\tan \theta =\dfrac{AB}{BC}$

Now, we will substitute the value of AB as 50m and BC as 50m. So,

$\tan \theta =\dfrac{50}{50}$

Hence, $\tan \theta =1$

As we know that $\tan 45{}^\circ =1$

So, $\tan \theta =\tan 45{}^\circ $

Hence, $\theta =45{}^\circ $

The angle is $45{}^\circ $.

Note: Instead of using trigonometric ratio one can also say that $AB=BC$. Thus $\Delta ABC$ is right angled isosceles so, $\angle ACB=45{}^\circ $ can be found.