Question

Find the angle of depression of a point on the ground, at 10 m distance from the base of the tower, from the top of the tower whose height is 10 m.

Answer 1

Hint: Here, we have to draw the figure to get the correct idea. Use the property of transversal that alternate interior angles are equal. Since two sides of the triangle are given, use $\tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side}$ to get the angle $\theta $, the angle of depression.

Complete step-by-step solution -
First, let us draw the figure.

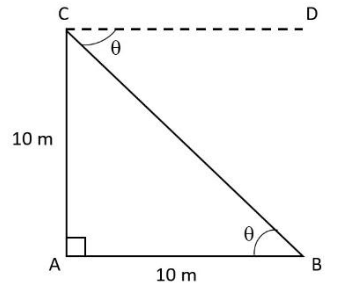
Here, we are given that the height of the tower, $AC=10\text{ }m$.
The distance between the point on the ground and base of the tower, $AB=10\text{ }m$
Now, we have to calculate the angle of depression of a point on the ground.
So, here let us consider the angle of depression as $\theta $.
From the figure we can say that $\angle DCB=\angle ABC=\theta $, since we know by the property of transversal that the alternate angles are equal.
Now consider the right angled triangle, $\vartriangle ABC$, where $AB=AC=10\text{ }m$
In the next step we have to calculate $\tan \theta $. i.e we can write:
$\tan \theta =\dfrac{opposite\text{ }side}{adjacent\text{ }side}$
From the figure we can say that the opposite side is $AC$, and the adjacent side is $AB$.
 Therefore, we will get:
$\begin{align}
  & \tan \theta =\dfrac{AC}{AB} \\
 & \tan \theta =\dfrac{10}{10} \\
 & \tan \theta =1 \\
\end{align}$
Next, by taking tan to the right side we get:
$\theta ={{\tan }^{-1}}1$
We know that $\tan {{45}^{\circ }}=1$, therefore ${{\tan }^{-1}}1={{45}^{\circ }}$
Hence, we can say that $\theta ={{45}^{\circ }}$
Therefore, we can say that the angle of depression of a point on the ground is ${{45}^{\circ }}$.

Note: For finding the angle of depression you should know which sides are given. Here the sides are opposite side and adjacent side, therefore you can use $\tan \theta $, instead if you use $\sin \theta $ or $\cos \theta $ you will get the wrong answer.