Question

How do you find the absolute extreme values of a function on an interval?

Answer 1

Hint: For the function $f\left( x \right)$ find all critical values of the function within the interval $\left[ a,b \right]$ by assuming $f'\left( x \right)=0$. Consider all the values within the interval $\left[ a,b \right]$ including the endpoints ‘a’ and ‘b’ and plug them into the function. The largest value will be the absolute maximum and the smallest value will be the absolute minimum.

Complete step by step answer:
We can solve this question by taking a suitable example.
Let the function be $f\left( x \right)={{x}^{3}}-12x+23$ on the interval $\left[ -5,3 \right]$
So, $f'\left( x \right)=3{{x}^{2}}-12$
Assuming $f'\left( x \right)=0$, we get
$\begin{align}
  & \Rightarrow 3{{x}^{2}}-12=0 \\
 & \Rightarrow 3\left( {{x}^{2}}-4 \right)=0 \\
 & \Rightarrow {{x}^{2}}-4=0 \\
 & \Rightarrow {{x}^{2}}=4 \\
 & \Rightarrow x=\pm \sqrt{4} \\
 & \Rightarrow x=\pm 2 \\
\end{align}$
Here we got two critical points as $2,-2$ both of which are in the interval $\left[ -5,3 \right]$
Now we need to find all the values including the critical points and the end points of the interval by plugging each one into $f\left( x \right)$.
$f\left( x \right)={{x}^{3}}-12x+23$
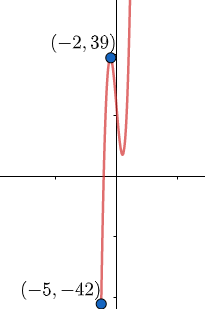
$f\left( -5 \right)={{\left( -5 \right)}^{3}}-12\times \left( -5 \right)+23=-125+60+23=-42$
$f\left( -2 \right)={{\left( -2 \right)}^{3}}-12\times \left( -2 \right)+23=-8+24+23=39$
$f\left( 2 \right)={{\left( 2 \right)}^{3}}-12\times \left( 2 \right)+23=8-24+23=7$
$f\left( 3 \right)={{\left( 3 \right)}^{3}}-12\times \left( 3 \right)+23=9-36+23=14$
From the above we can conclude that
The absolute maximum value$=39$ (at $x=-2$)
The absolute minimum value$=-42$ (at $x=-5$)
This is the required solution

Note: Only those critical points should be plugged into the function $f\left( x \right)$, which would lie inside the interval $\left[ a,b \right]$ . The endpoints ‘a’ and ‘b’ should also be considered. The ‘y’- coordinate of the maximum is it’s absolute maximum value and it’s ‘x’- coordinate is the point at which the function is attaining it’s maximum value. The ‘y’- coordinate of the minimum is it’s absolute minimum value and it’s ‘x’- coordinate is the point at which the function is attaining it’s minimum value. The above function can be graphed as