Question

Find packing fraction of three dimensional unit cell of AAAAA……………type hypothetical arrangement in which hexagonal packing is taken in layer.

Answer 1

Hint:To solve this we must first calculate the total area occupied by the spheres in the unit cell and the total area of the square unit cell. The packing efficiency can then be calculated by the ratio of area of spheres in the unit cell to the total area of the square unit cell.

 Complete step-by-step answer:
The structure of the hcp unit cell is as follows:

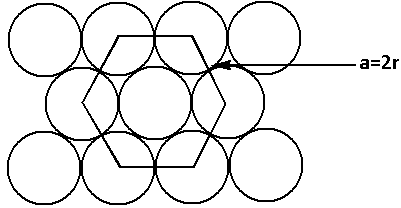
From the structure, we can see that
$a = 2r$ …… (1)
Where $a$ is the side of the face of the hexagon,
$r$ is the radius of the sphere.
We know the formula for the volume of the hexagon,
$V = \dfrac{{3\sqrt 3 }}{2}{a^2} \times h$
Where $V$ is the volume of the hexagon,
$a$ is the side of the face of the hexagon,
$h$ is the height of the hexagon and is equal to $2\sqrt {\dfrac{2}{3}} a$.
Thus, volume of hexagon is,
$V = \dfrac{{3\sqrt 3 }}{2}{a^2} \times 2\sqrt {\dfrac{2}{3}} a$
From equation (1), substitute $a = 2r$. Thus,
$V = \dfrac{{3\sqrt 3 }}{2}{\left( {2r} \right)^2} \times 2\sqrt {\dfrac{2}{3}} 2r$
$V = 24\sqrt 2 {r^3}$ …… (2)
Where $V$ is the volume of the hexagon,
$r$ is the radius of the sphere.
We know the formula for the volume of the sphere is,
$V = \dfrac{4}{3}\pi {r^3}$
Where $V$ is the volume of the sphere,
$r$ is the radius of the sphere.
In a hcp structure, there are a total six spheres. Thus, total volume of the spheres is,
$V = 6\left( {\dfrac{4}{3}\pi {r^3}} \right)$ …… (3)
The packing efficiency is the ratio of volume of spheres in the unit cell to the total volume of the cube cell. Thus, to calculate the packing efficiency divide equation (3) by equation (2). Thus,
${\text{Packing efficiency}} = \dfrac{{6\left( {\dfrac{4}{3}\pi {r^3}} \right)}}{{24\sqrt 2 {r^3}}}$
${\text{Packing efficiency}} = \dfrac{\pi }{{3\sqrt 2 }}$
Substitute $\pi = 3.14$. Thus,
${\text{Packing efficiency}} = \dfrac{{3.14}}{{3\sqrt 2 }}$
${\text{Packing efficiency}} = 0.7402$
Thus, the percentage packing efficiency is $0.7402 \times 100\% = 74.02\% $.

Thus, packaging fraction of three dimensional unit cell of AAAAA……………type hypothetical arrangement in which hexagonal packing is taken in layer is $74\% $.

Note: In hcp structure, each corner atom is shared by six unit cells and thus, the contribution of the corner atoms is two atoms. The tom at the centre is shared by two unit cells and thus, the contribution of the centre atom is one. One single cell contains three atoms. Thus, the total number of atoms in a hcp unit cell are six.