Question

Find m and n, If \[1125 = {3^m} \times {5^n}\].

Answer 1

Hint:
Factorisation is the process of writing any number as the product of its several factors usually prime factors.
Here, we use the factorization method to find factors of the given number \[1125\] and then we write this number in multiples of its factors. When the base is the same, powers can be added, therefore we group together all the powers having the same base.
* Here we use \[a \times a = {a^2}\] and \[a \times a \times a = {a^3}\] in prime factorization of \[1125\].
* Also prime numbers are the numbers which are only divisible by \[1\] and the number itself.

Complete step by step solution:
Given, \[1125 = {3^m} \times {5^n}\]
Factorise 1125, that is write 1125 as the product of its prime factors.
\[1125 = 3 \times 3 \times 5 \times 5 \times 5\].
We can draw a tree diagram of factors of a given number.

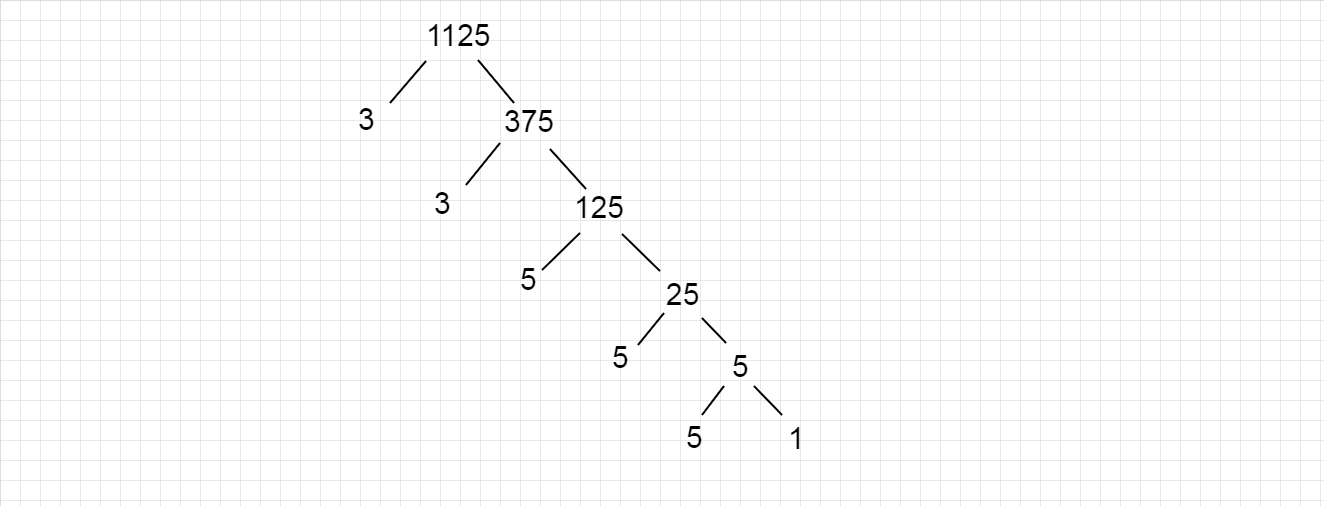
Since number of times \[3\] is multiplied to itself is \[2\] so, we write \[3 \times 3 = {3^2}\]
And number of times \[5\] is multiplied to itself is \[3\] so, we write \[5 \times 5 \times 5 = {5^3}\]
Write the product obtained in exponent form.
\[1125 = {3^2} \times {5^3}\]
Compare the obtained relation with the given \[1125 = {3^m} \times {5^n}\]
\[{3^m} \times {5^n} = {3^2} \times {5^3}\]
When the base is the same, we can equate the powers having the same base.
It can be observed that \[m = 2\] and \[n = 3\]

Note:
In these types of questions, factorisation is very important and the number must be represented as a product of only prime numbers. While factoring a number, students should always start with the lowest possibility of prime numbers so they cannot be factored further and we get base as a prime number.
Alternative method:
Another method to solve this question is hit and trial method where we can assume values of \[m\] and \[n\] to substitute them in \[1125 = {3^m} \times {5^n}\] again and again till we get our answer. But this method is very time consuming and it might be difficult to attain the answer in time because \[m\] and \[n\] can take many values.