
How do you find increasing, decreasing intervals, local max mins, concave up and down for $f\left( x \right)=\dfrac{{{x}^{2}}}{{{x}^{2}}+3}$ ?
Answer
533.4k+ views
Hint: Here we have been asked to find the increasing, decreasing intervals, local maximum and minimums, concave up and down for $f\left( x \right)=\dfrac{{{x}^{2}}}{{{x}^{2}}+3}$ . For that we will find the critical point which the value of $x$ for $\dfrac{d}{dx}f\left( x \right)=0$ and the inflection points which are the values of $x$ for which $\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)=0$ . We will evaluate $f\left( x \right)$ around critical points for increasing and decreasing intervals. Local maximum and minimum respectively exists at the values of $x$ for which $\dfrac{d}{dx}f\left( x \right)=0$ , $\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)<0$ and $\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)>0$ respectively.
Complete step by step solution:
Now considering from the question we have been asked to find increasing, decreasing intervals, local max mins, concave up and down for $f\left( x \right)=\dfrac{{{x}^{2}}}{{{x}^{2}}+3}$ .
For that we will first derivative the given function with respect to $x$
$\dfrac{d}{dx}f\left( x \right)=\dfrac{d}{dx}\left( \dfrac{{{x}^{2}}}{{{x}^{2}}+3} \right)\Rightarrow \dfrac{2x\left( {{x}^{2}}+3 \right)-{{x}^{2}}\left( 2x \right)}{{{\left( {{x}^{2}}+3 \right)}^{2}}}=\dfrac{6x}{{{\left( {{x}^{2}}+3 \right)}^{2}}}$
When $x=0$, then $\dfrac{d}{dx}f\left( 0 \right)=0$ this point is known as a critical point.
By substituting different values for $x$ we will have $f\left( 0 \right)=0$ , $f\left( 1 \right)=\dfrac{1}{4}$ and $f\left( -1 \right)=\dfrac{1}{4}$
So we can say that the function is decreasing in $\left( -\infty ,0 \right)$ and increasing in $\left( 0,\infty \right)$
Now we will differentiate the expression which we got by differentiating $f\left( x \right)$ with respect to $x$ again with respect to $x$ . Now we will have
$\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)=\dfrac{d}{dx}\left( \dfrac{6x}{{{\left( {{x}^{2}}+3 \right)}^{2}}} \right)\Rightarrow \dfrac{6{{\left( {{x}^{2}}+3 \right)}^{2}}-6x\left( 2\left( {{x}^{2}}+3 \right)2x \right)}{{{\left( {{x}^{2}}+3 \right)}^{4}}}=\dfrac{18\left( 1-{{x}^{2}} \right)}{{{\left( {{x}^{2}}+3 \right)}^{3}}}$
When $x=0$ then $\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)=\dfrac{18}{{{3}^{3}}}\Rightarrow \dfrac{2}{3}<0$
Therefore the local minimum exists at $x=0$ that is $f\left( 0 \right)=0$ . Moreover this is the absolute minimum for the function.
We will evaluate around the inflection points to know where the curve is concave up and concave down. When ${{f}^{''}}\left( x \right)<0$ in the interval the curve will be concave down and ${{f}^{''}}\left( x \right)>0$ in the interval the curve will be concave up.
Now we will find the Inflection points of $f\left( x \right)$ which are the values of $x$ for ${{f}^{''}}\left( x \right)=0$ . They are $x=\pm 1$ .
As ${{f}^{''}}\left( x \right)<0$ in $\left( -\infty ,1 \right)$ the curve will be concave down.
As ${{f}^{''}}\left( x \right)>0$ in $\left( -1,1 \right)$ the curve will be concave up.
As ${{f}^{''}}\left( x \right)<0$ in $\left( 1,\infty \right)$ the curve will be concave down.
Therefore the curve is concave up for $\left( -1,1 \right)$ and concave down for $\left( -\infty ,-1 \right)\cup \left( 1,\infty \right)$ .
Note:
While answering this question we should be sure with our concept and calculations we perform. This question can also be answered by clearly observing the graph of the function which looks as shown below:
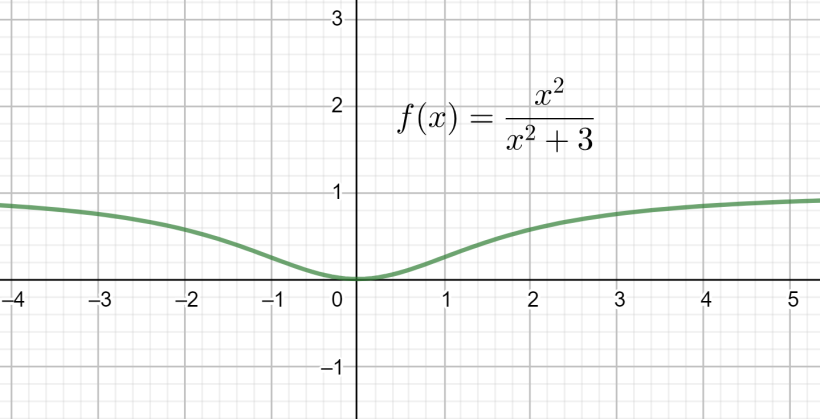
Complete step by step solution:
Now considering from the question we have been asked to find increasing, decreasing intervals, local max mins, concave up and down for $f\left( x \right)=\dfrac{{{x}^{2}}}{{{x}^{2}}+3}$ .
For that we will first derivative the given function with respect to $x$
$\dfrac{d}{dx}f\left( x \right)=\dfrac{d}{dx}\left( \dfrac{{{x}^{2}}}{{{x}^{2}}+3} \right)\Rightarrow \dfrac{2x\left( {{x}^{2}}+3 \right)-{{x}^{2}}\left( 2x \right)}{{{\left( {{x}^{2}}+3 \right)}^{2}}}=\dfrac{6x}{{{\left( {{x}^{2}}+3 \right)}^{2}}}$
When $x=0$, then $\dfrac{d}{dx}f\left( 0 \right)=0$ this point is known as a critical point.
By substituting different values for $x$ we will have $f\left( 0 \right)=0$ , $f\left( 1 \right)=\dfrac{1}{4}$ and $f\left( -1 \right)=\dfrac{1}{4}$
So we can say that the function is decreasing in $\left( -\infty ,0 \right)$ and increasing in $\left( 0,\infty \right)$
Now we will differentiate the expression which we got by differentiating $f\left( x \right)$ with respect to $x$ again with respect to $x$ . Now we will have
$\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)=\dfrac{d}{dx}\left( \dfrac{6x}{{{\left( {{x}^{2}}+3 \right)}^{2}}} \right)\Rightarrow \dfrac{6{{\left( {{x}^{2}}+3 \right)}^{2}}-6x\left( 2\left( {{x}^{2}}+3 \right)2x \right)}{{{\left( {{x}^{2}}+3 \right)}^{4}}}=\dfrac{18\left( 1-{{x}^{2}} \right)}{{{\left( {{x}^{2}}+3 \right)}^{3}}}$
When $x=0$ then $\dfrac{{{d}^{2}}}{d{{x}^{2}}}f\left( x \right)=\dfrac{18}{{{3}^{3}}}\Rightarrow \dfrac{2}{3}<0$
Therefore the local minimum exists at $x=0$ that is $f\left( 0 \right)=0$ . Moreover this is the absolute minimum for the function.
We will evaluate around the inflection points to know where the curve is concave up and concave down. When ${{f}^{''}}\left( x \right)<0$ in the interval the curve will be concave down and ${{f}^{''}}\left( x \right)>0$ in the interval the curve will be concave up.
Now we will find the Inflection points of $f\left( x \right)$ which are the values of $x$ for ${{f}^{''}}\left( x \right)=0$ . They are $x=\pm 1$ .
As ${{f}^{''}}\left( x \right)<0$ in $\left( -\infty ,1 \right)$ the curve will be concave down.
As ${{f}^{''}}\left( x \right)>0$ in $\left( -1,1 \right)$ the curve will be concave up.
As ${{f}^{''}}\left( x \right)<0$ in $\left( 1,\infty \right)$ the curve will be concave down.
Therefore the curve is concave up for $\left( -1,1 \right)$ and concave down for $\left( -\infty ,-1 \right)\cup \left( 1,\infty \right)$ .
Note:
While answering this question we should be sure with our concept and calculations we perform. This question can also be answered by clearly observing the graph of the function which looks as shown below:

Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




