Question

How do you find in radical form, the distance between the two points (-3,7) and (4,2)?

Answer 1

Hint: In this question, we are given two points and we need to find the distance between them in radical form. Therefore, we need to find the distance keeping the square root sign. For this we will generally use the distance formula. The distance between two points $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ is given by the formula, $ d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $ . We will solve the squares and add them but we will not solve the square root so that it remains in radical form.

Complete step by step answer:
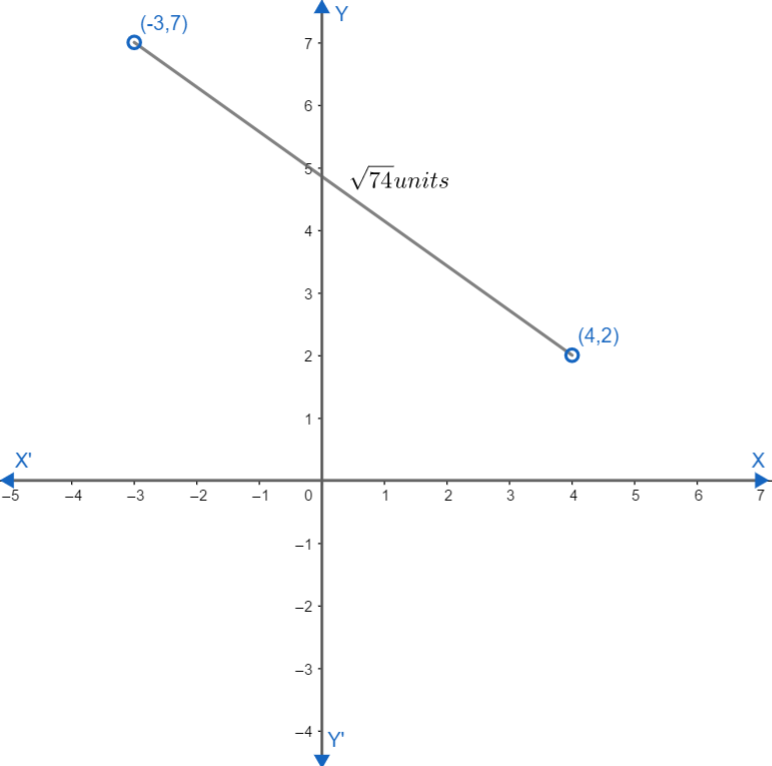
Here we are given two points as (-3,7) and (4,2). We need to find the distance between them. We are given points in the form as $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ and its distance will be as Cartesian units. Let us use distance formula for it.
We know that the distance d between two points $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ is given by the formula as $ d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $ .
Here we have points (-3,7) and (4,2). Comparing them with $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right) $ we have $ {{x}_{1}}=-3,{{x}_{2}}=4,{{y}_{1}}=7,{{y}_{2}}=2 $ .
Putting all these values in the formula we get $ d=\sqrt{{{\left( 4-\left( -3 \right) \right)}^{2}}+{{\left( 2-7 \right)}^{2}}} $ .
We can simplify it as $ d=\sqrt{{{\left( 4+3 \right)}^{2}}+{{\left( -5 \right)}^{2}}}\Rightarrow d=\sqrt{{{\left( 7 \right)}^{2}}+{{\left( -5 \right)}^{2}}} $ .
We know that negative sign gets absorbed in the square i.e $ -5\times -5=5\times 5=25 $ and we know $ 7\times 7=49 $ .
So putting in these values in the above equation we get $ d=\sqrt{49+25} $ .
Adding 49 with 25 gives us 74. So our equation become \[d=\sqrt{74}\].
So we have obtained our required distance. As we need to give the answer in radical form, so we will not remove the square root sign. Although we can simplify it, but we should not remove it completely.
Hence our required distance is \[\sqrt{74}\] units.

Note:
Students should note that, we can suppose any of the point as $ \left( {{x}_{1}},{{y}_{1}} \right)\text{ or }\left( {{x}_{2}},{{y}_{2}} \right) $ the answer will remain same because distance (-3, 7) to (4, 2) is same as the distance from (4,2) to (-3,7). We should note that, since 74 has factors 2 and 37 only which cannot come out of the square root, so our answer is already in simplified radical form.