Question

Find force in Newton which mass A exerts on mass B if B is moving forward right with \[3m/{{s}^{2}}\]. Also find mass A (All surfaces are smooth \[g=10m/{{s}^{2}}\])

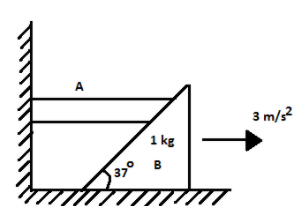
\[\begin{align}
  & A)5N,\dfrac{16}{31}kg \\
 & B)10N,\dfrac{31}{16}kg \\
 & C)10N,\dfrac{16}{31}kg \\
 & D)5N,\dfrac{31}{16}kg \\
\end{align}\]

Answer 1

Hint: Given that, mass B is moving with an acceleration due to the force exerted by the mass A. Draw the free body diagram of mass A and mass B. From this, we will get an idea about the forces acting on each body and we can find out the force exerted by mass A on B. To find the mass of A, first we need to calculate the acceleration of A. Then, by balancing the forces in vertical direction, we can calculate the mass.

Complete answer:

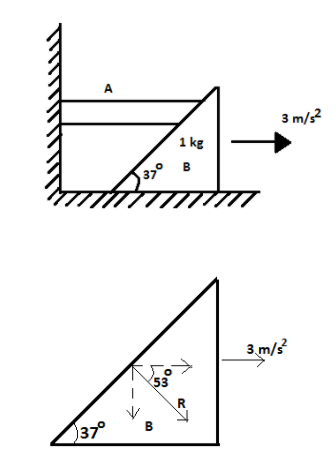
Free body diagram of mass B.
Here, mass B is moving with \[3m/{{s}^{2}}\] acceleration towards right. And the mass A is exerting a normal force \[R\] on B. Then, splitting the normal force in to its horizontal and vertical components, we get,
\[R\cos 53=m\times a\]
Substituting the values in above equation, we get,
\[R\cos 53=1\times 3=3\]
\[R\times \dfrac{3}{5}=3\]
\[R=5N\]
Force exerted by mass A exerts on mass B is \[5N\],
Now, let’s draw the vector diagram of acceleration of mass A and B.

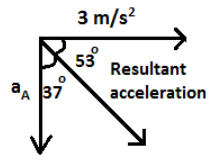
Here, mass B is moving with \[3m/{{s}^{2}}\] acceleration towards right and mass A can only move in the downwards.
Let, the mass A is moving with an acceleration \[{{a}_{A}}\].
The resultant acceleration of \[{{a}_{A}}\] and \[3m/{{s}^{2}}\] is,
\[{{a}_{A}}\cos 37=3\cos 53\]
\[{{a}_{A}}\times \dfrac{4}{5}=3\times \dfrac{3}{5}=\dfrac{9}{4}m/{{s}^{2}}\]
Acceleration of mass A,\[{{a}_{A}}=\dfrac{9}{4}m/{{s}^{2}}\]
Now, let’s draw the free body diagram of A.

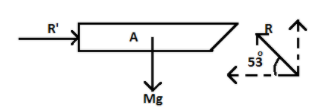
The mass A will experience a reaction force \[R'\] from the wall, and its weight is acting downwards \[mg\]. Also, it experiences the reaction force from mass B.
Balancing the forces along the vertical direction we get,
\[Mg-R\sin 53=M\times {{a}_{A}}\]
Where, \[M\]is the mass of A.
Substituting the values of \[g\] and \[{{a}_{A}}\], we get,
\[M\times 10-5\times \dfrac{4}{5}=M\times \dfrac{9}{4}\]
Then,
\[M=\dfrac{16}{31}kg\]
Mass of A is \[\dfrac{16}{31}kg\]

Therefore, the answer is option A.

Note:
Forces always come in pairs and these pairs are known as action-reaction forces. Identifying the action- reaction force pairs is a simple matter of identifying the two interacting bodies and explaining who is pushing on whom and in what direction. These two forces act against each other, which is explained by Newton’s third law.