Question

How do you find an asymptote of quadratic equations?

Answer 1

Hint: Now to check if the asymptotes of the function we will first check the value of function at which the function is not defined. Then we will check the end behavior of the function to find horizontal asymptote. Hence we will find the asymptote of the equation.

Complete step by step solution:
Now let us first understand the concept of asymptotes.
Asymptotes are lines which represent a value which a curve approaches but never reaches.
Now let us first understand two main types of asymptotes.
Horizontal asymptotes are lines which are parallel to the x axis and the curve tends to reach the value represented by the line but never reaches.
Now let us say as $x\to \infty $ the curve approaches value y = b.
Hence y = b is the horizontal asymptote of the curve.
Now similarly consider vertical asymptote.
Horizontal asymptotes are lines which are parallel to y axis and the curve tends to reach the value represented by the line but never reaches.
This case occurs when the function is not defined on some value x.
Now a function is not defined for the values where denominator is 0,
Hence we get a horizontal asymptote in this case.
Check the graph to understand.

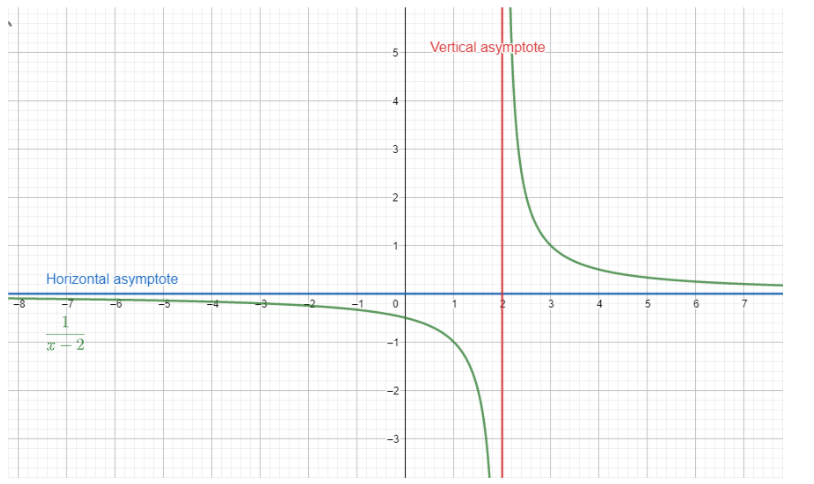
For example consider the example $y=\dfrac{1}{x-2}$ this curve will have a vertical asymptote at x = 2. And horizontal asymptote as y = 0.
Now consider the quadratic equation $a{{x}^{2}}+bx+c$.
Now the quadratic function is a polynomial and hence is defined on all values of x.
Hence we do not have vertical asymptote for the curve.
Now similarly as $x\to \infty $ we have $f\left( x \right)\to \infty $ .
Hence the curve reaches all the points.
Hence the function has no horizontal asymptote.
Hence the quadratic equation has no asymptote.

Note: Now if we have a function of the form $\dfrac{f\left( x \right)}{g\left( x \right)}$ where numerator and denominator are polynomials we have a vertical asymptote when $g\left( x \right)=0$ and horizontal asymptote at $\underset{x\to \infty }{\mathop{\lim }}\,\dfrac{f\left( x \right)}{g\left( x \right)}$ . Also note that asymptote is not a point but a line. We can say that the curve is parallel to the asymptote very close to the line.