Question

How do you find all the critical points to graph $9{{x}^{2}}-{{y}^{2}}-36x+4y+23=0$ including vertices, foci and asymptotes?
(a) By comparing the equation with the standard form
(b) Randomly guessing
(c) Drawing the graph
(d) All of the above

Answer 1

Hint: We can see that the equation given is a equation of a conic which is said to be a hyperbola. So, to get through this problem we are going to write down the standard form of the hyperbola and compare it with our given equation. Thus by analyzing we can get to our needed result quite comfortably.

Complete step-by-step answer:
Any hyperbola can be represented as,
$h(x,y)=\dfrac{{{(x-{{x}_{0}})}^{2}}}{a}-\dfrac{{{(y-{{y}_{0}})}^{2}}}{b}+c=0$
Now, we have, $9{{x}^{2}}-{{y}^{2}}-36x+4y+23-h(x,y)=0,\forall \{x,y\}\in {{\mathbb{R}}^{2}}$

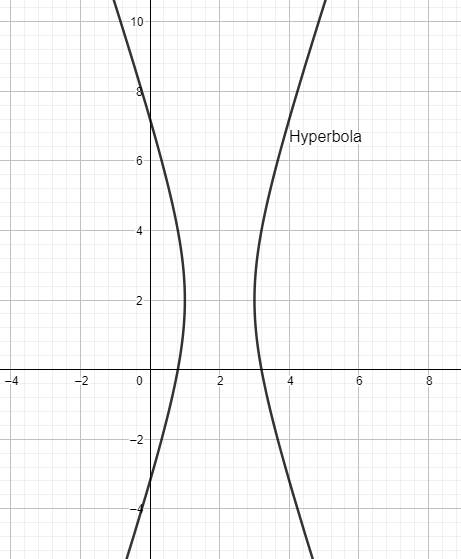
For a hyperbola, from this, we have the conditions,
\[c+\dfrac{x_{0}^{2}}{a}-\dfrac{y_{0}^{2}}{b}-23=0\] …..(1)
$\dfrac{2{{y}_{0}}}{b}-4=0$ …..(2)
$1-\dfrac{1}{b}=0$ …..(3)
$36-\dfrac{2{{x}_{0}}}{a}=0$ ….(4)
$\dfrac{1}{a}-9=0$ …..(5)
From equation 5 and 3, we have, $b=1,a=\dfrac{1}{9}$
Now from the value of a and equation 4, we have, ${{x}_{0}}=2$
Similarly from equation 2, we get, ${{y}_{0}}=2$
From all of these and equation 1, we are getting, $c=-9$ ,
Now putting the values in $h(x,y)$ , we get,
$9{{(x-2)}^{2}}-{{(y-2)}^{2}}-9=0$
And we also know for a hyperbola, we asymptotes are presented in the form,
$\sqrt{b}(x-{{x}_{0}})+\sqrt{a}(y-{{y}_{0}})=0,\sqrt{b}(x-{{x}_{0}})-\sqrt{a}(y-{{y}_{0}})=0$
Now, an asymptote is said to be,  An asymptote to a curve is a straight line, to which the tangent to the curve tends as the point of contact goes to infinity.
If this sounds confusing, you can think of an asymptote as follows: an asymptote to a curve is a straight line such that the perpendicular distance of a point P(x,y) on the curve from this line tends to zero as the point P goes to infinity (along some branch of the curve).
Thus, the asymptotes would be,
$(x-2)+\dfrac{1}{3}(y-2)=0,(x-2)-\dfrac{1}{3}(y-2)=0$
Hence, the correct option is, (a) By comparing the equation with the standard form.

Note: All hyperbolas share common features. A hyperbola consists of two curves, each with a vertex and a focus. The transverse axis is the axis that crosses through both vertices and foci, and the conjugate axis is perpendicular to it. A hyperbola also has asymptotes which cross in an “x”. The two branches of the hyperbola are on opposite sides of the asymptotes’ cross. The vertices and asymptotes can be used to form a rectangle, with the vertices at the centers of two opposite sides and the corners on the asymptotes. The centers of the other two sides, along the conjugate axis, are called the co-vertices. Where the asymptotes of the hyperbola cross is called the center.