Question

How do you find all solutions to ${x^5} + 243 = 0$?

Answer 1

Hint: First, subtract $243$ from both sides of the equation. Next, put $\theta = 0$ in ${e^{i\theta }} = {e^{i\left( {\theta + 2\pi k} \right)}}$. Next, take the 5th root of both sides of the equation to eliminate the exponent on the left side. Next, write $243$ as ${3^5}$ and simplify the result. Finally, find five possible values for $x$ by substituting in each possible value for $x$ by substituting in each value for $n$.

Formula used:
${e^{i\theta }} = {e^{i\left( {\theta + 2\pi k} \right)}}$ where $k$ is an integer
${e^{i\theta }} = \cos \theta + i\sin \theta $
${e^0} = 1$

Complete step by step solution:
Given equation: ${x^5} + 243 = 0$
We have to find all possible values of $x$ satisfying a given equation.
We will make use of the fact that ${e^{i\theta }} = {e^{i\left( {\theta + 2\pi k} \right)}}$ where $k$ is an integer (this is clear from Euler’s formula ${e^{i\theta }} = \cos \theta + i\sin \theta $), along with ${e^0} = 1$.
${x^5} + 243 = 0$
Subtract $243$ from both sides of the equation, we get
$ \Rightarrow {x^5} = - 243$
It can be written as
$ \Rightarrow {x^5} = - 243 \times 1$
Put $\theta = 0$ in ${e^{i\theta }} = {e^{i\left( {\theta + 2\pi k} \right)}}$.
$ \Rightarrow {x^5} = - 243{e^{i\left( {0 + 2\pi k} \right)}}$, $k \in \mathbb{Z}$
Take the 5th root of both sides of the equation to eliminate the exponent on the left side.
$ \Rightarrow x = {\left( { - 243{e^{2\pi ki}}} \right)^{\dfrac{1}{5}}}$, $k \in \mathbb{Z}$
Write $243$ as ${3^5}$.
$ \Rightarrow x = {\left( { - {3^5}{e^{2\pi ki}}} \right)^{\dfrac{1}{5}}}$, $k \in \mathbb{Z}$
It can be written as
$ \Rightarrow x = - 3{e^{\dfrac{{2\pi k}}{5}i}}$, $k \in \mathbb{Z}$
Due to the periodic nature of ${e^{i\theta }}$, we have that for any $k \in \mathbb{Z}$, ${e^{\dfrac{{2\pi k}}{5}i}} = {e^{\dfrac{{2\pi n}}{5}i}}$ for some $n \in \left\{ {0,1,2,3,4} \right\}$. Thus, we can find our five possible values for $x$ by substituting in each possible value for $x$ by substituting in each value for $n$.
$x \in \left\{ { - 3{e^{\dfrac{{2\pi n}}{5}i}}|n \in \left\{ {0,1,2,3,4} \right\}} \right\}$
Final solution: Hence, all solutions to ${x^5} + 243 = 0$ are $x \in \left\{ { - 3{e^{\dfrac{{2\pi n}}{5}i}}|n \in \left\{ {0,1,2,3,4} \right\}} \right\}$.

Note: Note that as ${e^{i\theta }} = \cos \theta + i\sin \theta $, and $\sin \left( {\dfrac{{2\pi n}}{5}} \right) = 0$ only when $n = 0$, the only real solution to the equation is
$ - 3{e^{\dfrac{{2\pi \times 0}}{5}i}} = - 3{e^0} = - 3$
In the above question, we can find the real solutions of a given equation by plotting the equation, ${x^5} + 243 = 0$ on graph paper and determine all its real solutions.

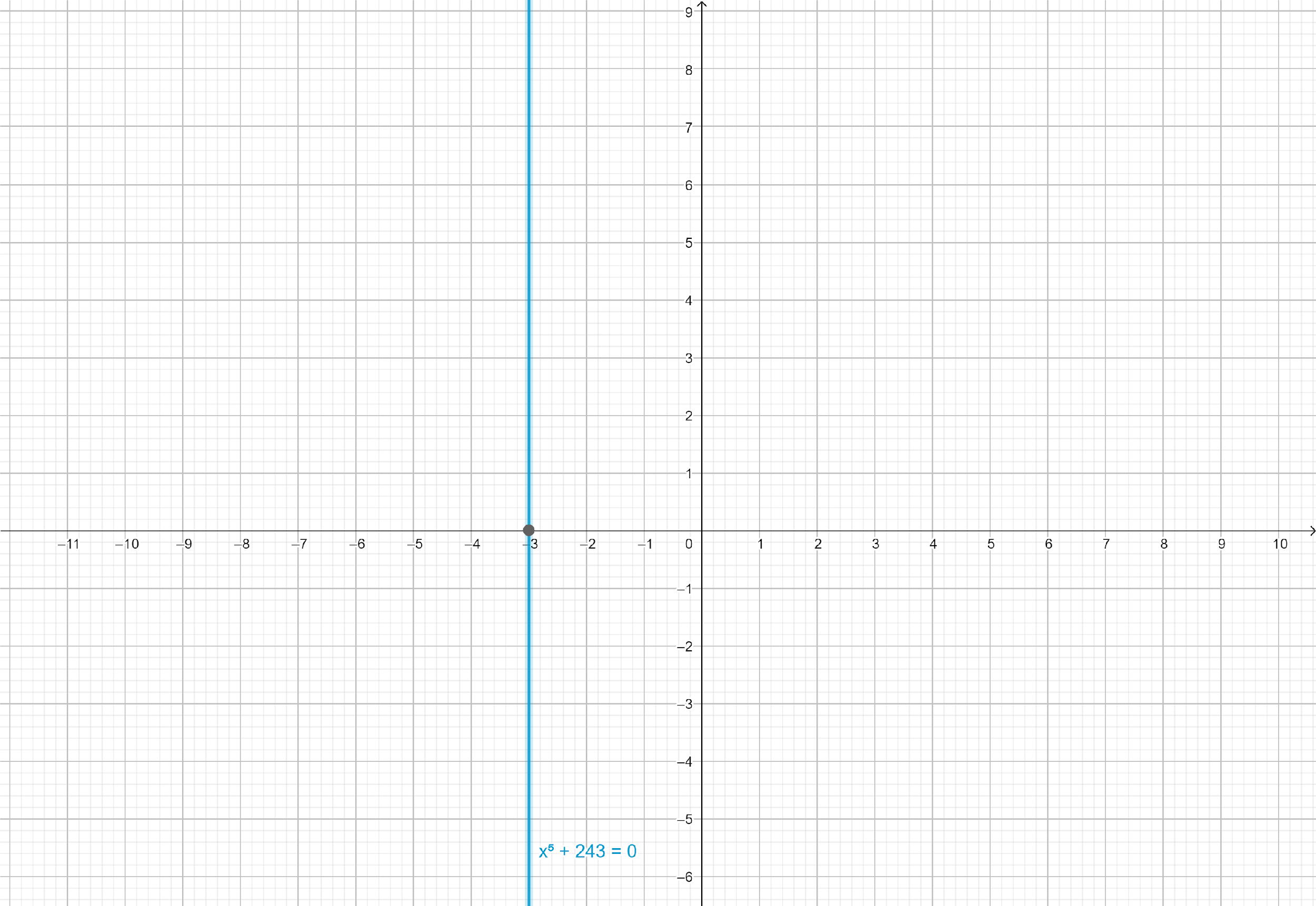
From the graph paper, we can see that $x = - 3$ is a solution to the given equation.
Hence, $x = - 3$ is the only real solution of the given equation.