Question

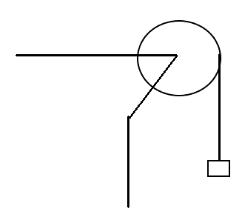
Figure shows a uniform disc with mass $ M = 2.4kg $ and radius $ R = 20cm $ , mounted on a fixed horizontal axle. A block of mass $ m = 1.2kg $ hangs from a massless cord which is wrapped around the rim of the disc. The tension in the cord is

(A) 12 N
(B) 20 N
(C) 24 N
(D) 6 N

Answer 1

Hint : Nothing is said about the cord being in equilibrium. We need to apply Newton’s second law on the block of mass. Then we can apply the rotational equivalent of Newton’s second law to the disc.

Formula used: In this solution we will be using the following formula;
 $ a = R\alpha $ where $ a $ is the tangential or linear acceleration of a rotating body, $ R $ is the radius of the rotating body, and $ \alpha $ is the angular acceleration of the rotating body.
 $ FR = I\alpha $ where $ F $ is force acting at the surface of a rotating body, $ I $ is the moment of inertia of the body, the product $ FR $ is known as torque.
 $ {I_d} = \dfrac{{M{R^2}}}{2} $ where $ {I_d} $ is the moment of inertia of a disc. $ M $ is the mass the disc
 $ {F_{NET}} = ma $ where $ {F_{NET}} $ is the net force acting on a body, $ m $ is the mass and $ a $ is the acceleration of the body.

Complete step by step answer:
A block of mass $ 1.2kg $ is attached to a string attached to a disc mounted on an axle. We are to determine the tension on the string. To do so, we must calculate, perform newton’s second law analysis on the block, and perform the rotational equivalent of the disc.
For the disc,
 $ FR = I\alpha $ where $ F $ will be the force on the string equal to the tension, hence,
 $ T = \dfrac{{I\alpha }}{R} $
But the moment of inertia of a disc $ I = \dfrac{{M{R^2}}}{2} $
And from $ a = R\alpha $ where $ a $ is the tangential or linear acceleration of a rotating body, $ R $ is the radius of the rotating body, and $ \alpha $ is the angular acceleration of rotating body, we have that
 $ \alpha = \dfrac{a}{R} $
Then, inserting these into $ T = \dfrac{{I\alpha }}{R} $ , we have
 $ T = \dfrac{{M{R^2}}}{{2R}}\dfrac{a}{R} = \dfrac{{Ma}}{2} $
 $ \Rightarrow a = \dfrac{{2T}}{M} $
Now, performing Newton’s law on the block we have
 $ {F_{NET}} = ma $ where $ {F_{NET}} $ is the net force acting on a body, $ m $ is the mass and $ a $ is the acceleration of the body.
Then,
 $ mg - T = ma $
By replacing $ a $ with $ \dfrac{{2T}}{M} $ , we have
 $ mg - T = m\left( {\dfrac{{2T}}{M}} \right) $
Hence,
 $ mg = m\left( {\dfrac{{2T}}{M}} \right) + T $
 $ \Rightarrow mg = T\left( {\dfrac{{2m}}{M} + 1} \right) $
Then by dividing both sides by $ \left( {\dfrac{{2m}}{M} + 1} \right) $ , we have
 $ T = \dfrac{{mg}}{{\left( {\dfrac{{2m}}{M} + 1} \right)}} $
Hence, by inserting all known values, we get
 $ T = \dfrac{{1.2\left( {10} \right)}}{{\left( {\dfrac{{2\left( {1.2} \right)}}{{2.4}} + 1} \right)}} = \dfrac{{12}}{{1 + 1}} = \dfrac{{12}}{2} $
Hence,
 $ T = 6N $
Hence, the correct answer is option D.

Note:
For clarity, we do not perform a Newton’s law analysis on the disc because it is already placed on an axle. Hence, the disc cannot be in linear motion but only rotational motion about its centre due to the tension on the string.