Question

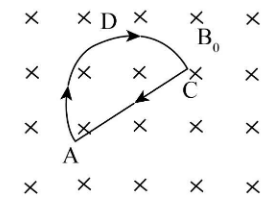
Figure shows a conducting loop ADCA carrying current i and placed in a region of uniform magnetic field \[{B_0}\]. The part ADC forms a semicircle of radius R. The magnitude of force on the semicircle part of the loop is equal to

(1) \[\pi Ri{B_0}\]
(2) Zero
(3) \[2\pi Ri{B_0}\]
(4) \[2iR{B_0}\]

Answer 1

Hint:To solve this problem, one should remember the relation between the magnetic force due to a uniform magnetic field on a current-carrying straight line and its length, current flowing through it, and magnetic field. We will replace the length of line AC in terms of the semi-circular loop radius to find the final expression for the magnetic force.

Complete step by step answer:
We know that force due to a uniform magnetic field in a closed loop is equal to zero. Therefore, we can say that the force in loop ADC is equal to force on straight-line AC. Hence we can write the expression force of semi-circular loop ADC as below:
\[F = i{B_0}l\]……(1)
Here i is the current flowing through the loop, B is the uniform magnetic field, and l is the straight line AC length.
On closely observing the given figure, we find that the length of straight-line AC is equal to the semi-circular curve ADC diameter.
\[l = D\]……(2)
Here D is the diameter of the semi-circular curve ADC.
We know that diameter of the semi-circular curve is twice its radius, so we can write:
\[D = 2R\]
Here R is the radius of the given semi-circular curve.
We will substitute \[2R\] for D in equation (2) to find the length of straight-line AC in radius.
\[l = 2R\]
Now we will substitute \[2R\] for l in equation (1) to get the final expression for force in the loop ADC due to a uniform magnetic field.
\[
F = i{B_0}\left( {2R} \right)\\
\therefore F = 2iR{B_0}
\]
Hence,option (4) is the correct answer.

Note: Alternate method: We can write the general expression for the magnetic field, and we can integrate it over the given area. Later we can substitute it in the expression for magnetic force in the semi-circular loop.