Question

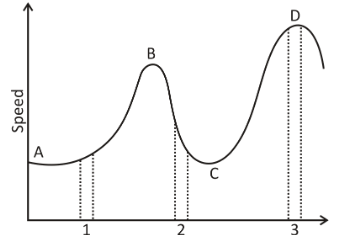
Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs $v$ and $a$ in three intervals. What are the acceleration at the points A, B, C and D?

Answer 1

Hint:First let us see what a speed-time graph is and what it signifies: Speed-time graphs are very useful when explaining the motion of an object. The region below the speed-time graph reflects the distance travelled. This is the velocity time graph of an object travelling along a straight line to the north. The displacement of this object is the time graph velocity field.

Complete answer:
The speed-time graph of the particle provides details on the acceleration of the particle. The amplitude of the total acceleration of the particle depends on the slope of the graph at the same interval. The slope of the graph at interval $2$ is maximal and is in a negative direction. It thus has the highest amplitude of the normal acceleration.

On the other hand, the average speed depends on the size of the particle speed. As the time periods are about the same, the average speed would depend on the degree of the speed. The speed of the particle shall be the limit at interval 3 and shall also have the maximum average speed.For all the intervals, the speed signs are positive, while the acceleration depends on the graph's slope.

-As the gradient is positive in the interval $1$, so the acceleration is positive.
-As the gradient is negative in the interval $2$, so the acceleration is negative.
-As the gradient is positive in the interval $3$, so the acceleration is positive.
The slope of the speed-time graph is parallel to the time axis at the four instants of A, B, C & D. It implies that zero is the slope of the line.

Hence,the acceleration of the particle will also therefore be zero at A, B, C & D.

Note:Constant velocity means that zero is the acceleration. For a given time interval, the difference in velocity equals the field over that interval under the acceleration graph. The velocity does not shift in this situation, because there will be no field under the graph of acceleration.