Question

Figure below shows the diagram drawn on a square sheet of paper, constructing a square pyramid. What is the length of a side of the square sheet of paper taken?
The figure drawn in the square paper is cut out and folded to make a square pyramid.
What would be the height of that pyramid?

Answer 1

Hint:
Here, we will find the length of a square sheet of paper and then the height of the pyramid. We will use Pythagoras theorem to find the height of the triangle and then by using the properties of the square, we will find the length of the square. Then by adding all the lengths of the square and length of the triangle, we will find the length of a square sheet of paper. We will use the height of the pyramid formula to find the height of the pyramid. Pyramid is defined as a shape of a polygon at the base and three or more triangles which meet at the top.

Formula Used:
Height of the Pyramid is given by the formula \[h = \sqrt {{l^2} - {r^2}} \] where \[l,r\] be the slant height and the radius respectively.

Complete Step by Step Solution:

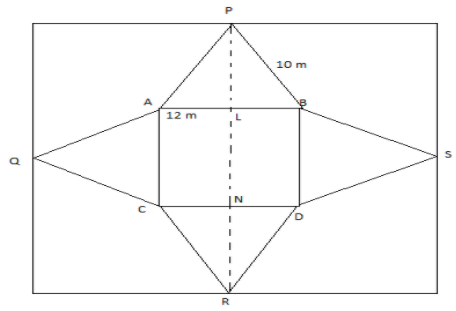
We are given that \[BP = 12m\], \[AB = 10m\]
Since \[L\] is the midpoint of the square, we get \[AL = BL = 6m\]
Now, in a right angle triangle \[\Delta PLB\], by using the Pythagoras theorem, we will find the height of the triangle i.e., \[PL\]
\[P{B^2} = L{B^2} + P{L^2}\]
Now, by substituting \[BP = 10m\] and \[BL = 6m\] in the above equation, we get
\[ \Rightarrow {10^2} = {6^2} + P{L^2}\]
\[ \Rightarrow P{L^2} = {10^2} - {6^2}\]
Applying the exponent on the terms, we get
\[ \Rightarrow P{L^2} = 100 - 36\]
\[ \Rightarrow P{L^2} = 64\]
Taking square root on both sides we get
\[ \Rightarrow PL = \sqrt {64} \]
\[ \Rightarrow PL = 8m\]
Now, we know that the sides of similar triangles are equal i.e.\[PL = NR = 8m\] .
Since \[ABCD\] is a square, we know that all the sides of a square are equal.
So, we get \[AB = BC = CD = DA = 12m\]
Now, we will find the length of the side of a square sheet of paper taken by adding the length of the square and the height of the two triangles.
Length of the side of square sheet of paper \[ = PL + LN + NR\]
Substituting \[PL = 8\], \[LN = 12\] and \[NR = 8\] in the above equation, we get
\[ \Rightarrow \] Length of the side of square sheet of paper \[ = 8 + 12 + 8\]
\[ \Rightarrow \] Length of the side of square sheet of paper \[ = 28m\]
Now, we will find the height of the pyramid.
By substituting the values of \[l = 8\] and \[r = 6\] in the formula \[h = \sqrt {{l^2} - {r^2}} \], we get
\[h = \sqrt {{8^2} - {6^2}} \]
Applying the exponent of the terms, we get
\[ \Rightarrow h = \sqrt {64 - 36} \]
Subtracting the terms, we get
\[ \Rightarrow h = \sqrt {28} \]
Rewriting the terms, we get
\[ \Rightarrow h = \sqrt {4 \times 7} \]
\[ \Rightarrow h = 2\sqrt 7 m\]

Therefore, the length of the side of a paper taken is \[28m\] and the height of the pyramid is \[2\sqrt 7 m\].

Note:
We know that the Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Pythagoras theorem is applicable only in the case of a right-angled triangle. The slant height is defined as the distance between the vertex of a pyramid to any point that lies on the circumference of the base. Here we might get confused and take \[PL = 10\] which will give us the wrong answer. The 10 m is the slant height and not the height of PL.